题目内容
4.1998年1月发射的“月球勘探者号”空间探测器,运用最新科技手段对月球近距离勘测,在月球重力分布、磁场分布及元素测定方面取得了最新成果.(1)探测器在一些环形山中发现了质量密集区,当飞越这些重力异常区时,通过地面大口径射电望远镜观察,轨道参数发生了微小变化,这些变化是BC
A.速度变小 B.速度变大 C.半径变小 D.半径变大
(2)月球上的磁场极其微弱,探测器通过测量运动电子在月球磁场中的轨迹来推算磁场强弱分布.如图2-4-13所示是探测器通过月球a、b、c、d四个位置时,电子运动轨道的照片,设电子速率相同,且与磁场方向垂直,则其中磁场最强的位置是A,图A中电子轨道半径为10 cm,电子的比荷为1.8×1011C/kg,速度为90 m/s,则a点的磁感应强度为5×10-9T.

分析 (1)当探测器在飞越月球上一些环形山中的质量密集区上空时,月球的重心上移,导致轨道半径减小,根据万有引力提供向心力判断速率的变化.
(2)电子在月球磁场中做圆周运动时,根据半径公式r=$\frac{mv}{Bq}$分析得知,半径与磁感应强度成反比,由图分析轨迹半径的大小,即可得到磁感应强度的大小.
解答 解:(1)当探测器在飞越月球上一些环形山中的质量密集区上空时,月球的重心上移,轨道半径减小,根据$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,解得v=$\sqrt{\frac{GM}{r}}$,r减小,则v增大.故AD错误,BC正确.
故选:BC
(2)电子在月球磁场中做匀速圆周运动,洛伦兹力提供向心力,则有:
$Bqv=m\frac{{v}^{2}}{r}$
解得:半径为r=$\frac{mv}{Bq}$,
m、q、v相同,则半径r与磁感应强度B成反比.由图看出,A照片中电子轨迹半径最小,则磁感应强度B最大,即磁场最强.
B=$\frac{mv}{rq}=\frac{90}{1.8×1{0}^{11}×0.1}=5×1{0}^{-9}T$
故答案为:(1)BC;(2)A;5×10-9
点评 (1)解决本题的关键掌握万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$;
(2)本题考查运用物理知识分析实际问题,背景较新,但落点较低,实质是带电粒子在磁场中圆周运动半径公式r=$\frac{mv}{Bq}$的直接应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14. 在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表A、V1、V2、V3,的示数分别用I,U1、U2、U3和表示,电表A、V1、V2、V3示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )
在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表A、V1、V2、V3,的示数分别用I,U1、U2、U3和表示,电表A、V1、V2、V3示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )
 在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表A、V1、V2、V3,的示数分别用I,U1、U2、U3和表示,电表A、V1、V2、V3示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )
在如图所示电路中,闭合电键S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表A、V1、V2、V3,的示数分别用I,U1、U2、U3和表示,电表A、V1、V2、V3示数变化量的大小分别用△I、△U1、△U2和△U3表示.下列说法正确的是( )| A. | $\frac{U_1}{I}$比值不变,$\frac{{△{U_1}}}{△I}$比值不变 | B. | $\frac{U_2}{I}$比值变大,$\frac{{△{U_2}}}{△I}$比值变大 | ||
| C. | $\frac{U_2}{I}$比值变大,$\frac{{△{U_2}}}{△I}$比值不变 | D. | $\frac{U_3}{I}$比值变大,$\frac{{△{U_3}}}{△I}$比值不变 |
19.如图所示,一电子束沿电流方向运动,则电子束将( )


| A. | 偏向电流 | B. | 偏离电流 | C. | 无偏转 | D. | 不能确定 |
16.磁性减退的磁铁需要充磁,充磁的方式有两种,如图甲、乙所示.甲是将条形磁铁穿在通电螺线管中,乙是将条形磁铁夹在电磁铁之间.a、b和c、d接直流电源,正确的接线方式是( )
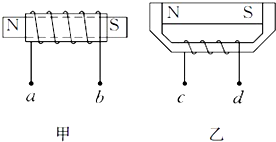

| A. | a接电源正极,b接负极 | B. | a接电源负极,b接正极 | ||
| C. | c接电源正极,d接负极 | D. | c接电源负极,d接正极 |
15.下列关于电容器的叙述正确的是( )
| A. | 电容器是储存电荷和电能的容器,只有带电的容器才称为电容器 | |
| B. | 任何两个彼此绝缘而又相互靠近的导体,就组成了电容器,跟这两个导体是否带电无关 | |
| C. | 电容器所带的电荷量是指每个极板所带电荷量的绝对值 | |
| D. | 电容器充电过程是将其他形式的能转变成电容器的电场能并储存起来;电容器放电过程,是将电容器储存的电场能转化为其他形式的能 |

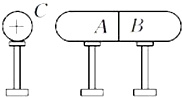 如图所示,两个互相接触的导体A和B,靠近带正电的导体球C放置,三者均有绝缘支架,若先将C移走,再把A、B分开,则 A不带电,B不带电;若先将A、B分开,再移走C,则A带负电,B带正电.
如图所示,两个互相接触的导体A和B,靠近带正电的导体球C放置,三者均有绝缘支架,若先将C移走,再把A、B分开,则 A不带电,B不带电;若先将A、B分开,再移走C,则A带负电,B带正电.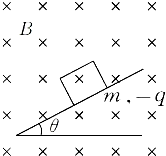 将倾角为θ的光滑绝缘斜面放置在一个足够大的、磁感应强度为B、方向垂直纸面向里的匀强磁场中.一个质量为m、带电荷量为-q的小滑块,在竖直平面内沿斜面由静止开始下滑,如图所示,问:经过多少时间,带电滑块将脱离斜面?
将倾角为θ的光滑绝缘斜面放置在一个足够大的、磁感应强度为B、方向垂直纸面向里的匀强磁场中.一个质量为m、带电荷量为-q的小滑块,在竖直平面内沿斜面由静止开始下滑,如图所示,问:经过多少时间,带电滑块将脱离斜面?