Question

【题目】如图所示，始终绷紧的水平传送带以v=4.0m/s的恒定速率沿顺时针方向转动，质量M=10kg的平板车停在传送带的右端.现把质量m=5.0kg可视为质点的行李箱轻轻放到距传送带右端x0=5.0m位置．行李箱与传送带、平板车间的动摩擦因数分别为，平板车与水平地面间的动摩擦因数为.（不计空气阻力，g=10m/s2）试求：

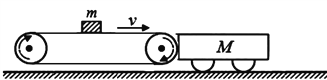
(1)行李箱在传送带上运动的时间t;

(2)行李箱滑到平板车上后，在相对滑动过程中，行李箱及平板车的加速度大小分别是多少？

(3)若行李箱由传送带滑到平板车上时速度不变，要想行李箱恰不从平板车上滑出，平板车的最小长度.（结果可用分数表示）

Answer 1

【答案】(1)2.25s (2), (3)

【解析】

(1)行李箱在传送带上先做初速度为零的匀加速直线运动后做匀速直线运动，应用牛顿第二定律求出加速度，应用运动学公式求出行李箱的运动时间.

(2)行李箱滑上平板车后做匀减速直线运动，平板车做匀加速直线运动，当行李箱滑到平板车右端且两者速度相等时，行李箱恰好没有离开平板车，此时平板车最短，应用牛顿第二定律与运动学公式可以求出平板车的最小长度.

(1)对行李箱，由牛顿第二定律得：

行李箱匀加速运动的时间为：

匀加速的位移为：

行李箱在传送带匀速的时间为：

行李箱在传送带上运动的时间为：t=t1+t2=2.25s；

(2)行李箱滑到平板车后，当行李箱速度大于平板车速度时，行李箱做减速运动，

由牛顿第二定律，对行李箱有：

对平板车有：

(3)设行李箱经时间t3恰好到达平板车右端且两者速度刚好相等，由匀变速直线运动的速度公式得：v-a2t3=a3t3

解得：

平板车的速度：

平板车的最小长度：

解得：