题目内容
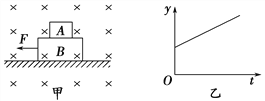
【题目】质量m=1kg的物体置于倾角θ=37°的足够长固定斜面上，对物体施加平行于斜面向上的恒力F，作用时间t1=1s后撤去恒力，物体运动的部分v﹣t图象如图乙所示，取g=10m/s2 ， ．
试求：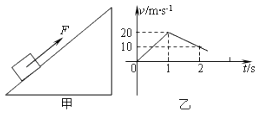
（1）物体沿斜面上滑过程中的两个加速度．
（2）恒力F的大小和斜面与物体间的动摩擦因数u
（3）物体t=4s时的速度v．
【答案】
（1）解：根据v﹣t图象可知，加速阶段加速度为：
a1= 
=20m/s2，
减速阶段加速度为：
a2= 
=﹣10m/s2，
答：物体沿斜面上滑过程中的两个加速度分别为20m/s2和﹣10m/s2
（2）解：根据牛顿第二定律可知，
加速上升过程有：F﹣mgsinθ﹣μmgcosθ=ma1
减速上升过程有：﹣mgsinθ﹣μmgcosθ=ma2
联立解得：F=30N，μ=0.5
答：恒力F的大小为30N，斜面与物体间的动摩擦因数u为0.5
（3）解：由题意可知，mgsinθ=6N＞μmgcosθ=4N，可知物体减速为零后可以匀加速下滑，
又 1s后物体做匀减速，3s末的速度为 V3=V1+at=20+（﹣10）2m/s=0m/s，即3s末速度为零，
则 3s到4s这1s的时间间隔内物体沿斜面向下做匀加速直线运动，设加速度为a3，由牛顿第二定律得：
mgsinθ+μmgcosθ=ma3
代入数据解得：a3=﹣2m/s2
由速度时间关系可知，4s时速度为：
V4=V3+at=0+（﹣2）×1m/s=﹣2m/s，方向沿斜面向下
答：物体t=4s时的速度v为2m/s，方向向下
【解析】（1）根据速度时间图像的含义，求出两个阶段，加速度的大小。
（2）根据牛顿第二运动定律，对加速和减速过程列方程组求解。
（3）牛顿第二运动定律先求出三秒到四秒加速度，再根据匀变速直线运动规律求初速度。
【考点精析】通过灵活运用匀变速直线运动的速度、位移、时间的关系，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值即可以解答此题．
