��Ŀ����
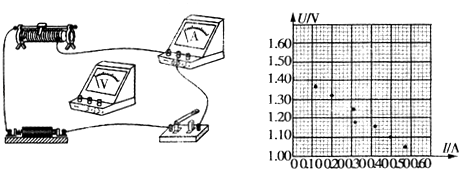
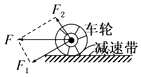
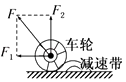
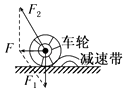
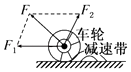
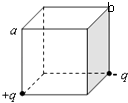
����Ŀ����ͼ��ʾ��һ����ΪM=4kg����ΪL=1.5m��ľ�����ˮƽ�����ϣ���֪ľ�������䶯Ħ������Ϊ0.1���ڴ�ľ����Ҷ��ϻ���һ����Ϊm=1kg�����飬����С����Ϊ�ʵ㣬ľ���Ȳ��ƣ����ľ��ͻȻʩ��һ��ˮƽ���ҵ�������
![]()
��1��������������ľ����Ħ����������Ϊ8N����С���龭�ʱ�佫�뿪ľ�壿
��2����������ľ���Ķ�Ħ������Ϊ0.2������������Ķ�Ħ������Ϊ0.1��Ҫ��С����Եص���λ�Ʋ�����1.5m����ʩ����ľ��ˮƽ���ҵ���������ʲô��������g=10m/s2��
���𰸡���1��2 s��2��F��39N
���������������������������ľ����Ħ������ľ���˶�ʱ����������ڵ��治��������ţ�ٵڶ��������ľ��ļ��ٶȣ��Ӷ������˶�ѧ��ʽ���ľ������λ��ΪLʱ�����ʱ�䣬��С�����뿪ľ���ʱ��������ţ�ٵڶ����ɷֱ����������ľ���ϡ������ڵ������˶��ļ��ٶȣ��Լ�ľ���˶��ļ��ٶȣ�ץס�������λ�Ƶ�����ľ�����˶�ʱ����ڵ����λ�ƺ��ڵ��������ȼ���ֱ���˶���λ��֮�ͣ��Լ��������ľ���λ�Ƶ��������λ����ľ���λ��֮������˶�ѧ��ʽ��������ķ�Χ��
��1���Գ�ľ����������������ţ�ٵڶ������У� ![]()
�������ݽ�ã�a1=0.75 m/s2
ľ���˶���λ��Ϊ�� ![]()
�������ݽ�ã�t=2 s
��2����Ե��棺������ľ����ʱ������ţ�ٵڶ����ɿɵü��ٶ�Ϊ��a1=��1g=2m/s2
�����ڵ�����ʱ����ţ�ٵڶ������У�a2=��2g=1m/s2
ľ��Ե�����ٶ�������ţ�ٵڶ������У� ![]()
����f1=��1mg��f2=��2(m+M)g
������Ե���λ����2a1x1=v12 ��2a2x2=v12
λ�ƹ�ϵ������ x2+ x1��1.5m
��������ľ���ϻ���ʱ��Ϊt1��������Ե���λ��![]()
ľ��Ե���λ��![]() ������x= x1+L
������x= x1+L
�������Ͻ�ã� F��39N