题目内容
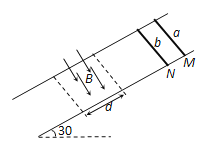
【题目】如图所示,两根互相平行的光滑金属导轨倾斜放置,导轨平面与水平面夹角为30°,导轨间距L=1 m,电阻忽略不计。垂直导轨的虚线间有一匀强磁场,磁感应强度大小B=0.5 T,方向垂直导轨平面向下,磁场区域的宽度d=0.8 m。导体棒a质量ma= 0.25 kg,电阻Ra=0.5 Ω;导体棒b的质量mb= 0.05 kg,电阻Rb=1.5 Ω,它们分别从图中M、N处同时由静止释放,b恰好匀速穿过磁场区域,且当b刚穿出磁场时a正好进入磁场,重力加速度g=10 m/s2,不计a、b棒之间的相互作用,导体棒始终与导轨垂直且与导轨接触良好,求:
(1)b棒刚进入磁场时的速度大小;
(2)a棒刚进入磁场时两端的电压;
(3)为保持a棒以进入时的加速度做匀加速运动,需对a棒施加平行于导轨向下的外力F作用,求F随时间t的变化关系。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)当b棒刚进入磁场时,产生的感应电动势为E=BLv┈┈┈┈┈┈┈┈①
由闭合电路欧姆定律得,通过导体棒b的电流为E=I(Ra+Rb) ┈┈┈┈┈┈┈②
由力学平衡条件得 ![]() ┈┈┈┈┈┈┈┈┈┈┈③
┈┈┈┈┈┈┈┈┈┈┈③
代入数据解得:v=2m/s┈┈┈┈┈┈┈┈④
(2)b棒在磁场运动的时间为t,则有:d=vt┈┈┈┈┈┈┈┈┈┈⑤
a、b棒在磁场外运动时,速度总是相等的,b棒进入磁场后,a棒继续加速t时间而进入磁场,a棒进入磁场时的速度为va,则
![]() =4m/s┈┈┈┈┈┈┈┈⑥
=4m/s┈┈┈┈┈┈┈┈⑥
此时,a棒产生的电动势为Ea=BLva┈┈┈┈┈┈⑦
其两端的电压为![]() ┈┈┈┈┈┈┈┈⑧
┈┈┈┈┈┈┈┈⑧
(3)a棒刚进入磁场时的加速度为 ![]() ┈┈┈┈┈┈┈┈⑨
┈┈┈┈┈┈┈┈⑨
代入数据解得a=3m/s2┈┈┈┈┈┈┈┈⑩
导体棒运动时间t时刻速度v2为 ![]() ┈┈┈┈┈┈┈┈
┈┈┈┈┈┈┈┈
此时电流的表达式为 ![]() ┈┈┈┈┈┈┈┈
┈┈┈┈┈┈┈┈
施加平行于导轨平面向上的作用力F后,由牛顿第二定律得
![]() ┈┈┈
┈┈┈
代入数据后解得:![]() ┈┈┈┈┈┈
┈┈┈┈┈┈

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案