题目内容
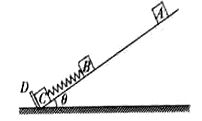
【题目】(10分)如图所示，矩形ABCD为长方体水池横截面，宽度d=6m，高h＝(2
+1)m，水池里装有高度为h′＝2
m、折射率为n＝
的某种液体，在水池底部水平放置宽度d′=5m的平面镜，水池左壁高b＝
m处有一点光源S，在其正上方放有一长等于水池宽度的标尺AB，S上方有小挡板，使光源发出的光不能直接射到液面，不考虑光在水池面上的反射，求:
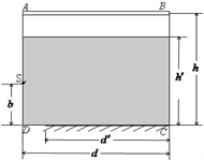
①在此横截面上标尺上被照亮的长度x1
②液面上能射出光线部分的长度x2
【答案】2m 2.2m
【解析】
试题①S发出的临界光线光路如图所示，
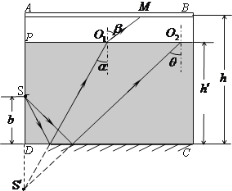
由几何关系有 sinα=
(1分)
根据折射定律 
＝n (1分)
则β=45°
此横截面上标尺上被照亮的长度
x1=d(b+h′)tanα(hh′)tanβ (2分)
解得x1=2m (1分)
②设此液体的临界角为θ，则
sinθ＝
(1分)
则θ=45° (1分)
则液面上能射出光线部分的长度
x2=
=(b+h′)(tanθtan300) (2分)
解得x2=
=2.2m (1分)
练习册系列答案
寒假大串联黄山书社系列答案
相关题目
