Question

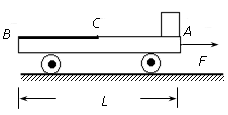
（20分）如图所示，光滑水平地面上停着一辆平板车，其质量为，长为L，车右端（A点）有一块静止的质量为的小金属块。金属块与车间有摩擦，与中点C为界， AC段与CB段动摩擦因数不同。现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，即撤去这个力。已知撤去力的瞬间，金属块的速度为，车的速度为，最后金属块恰停在车的左端（B点）。如果金属块与车的AC段间的动摩擦因数为，与CB段间的动摩擦因数为，求与的比值。

   

Answer 1

解析：

由于金属块和车的初速度均为零，且经过相等时间加速后车速是金属块速度的2倍，则在此过程中车的加速度是金属块加速度的两倍。

金属块加速度   ①

则车的加速度   ②

在此过程中金属块位移     ③   

车的位移   ④

由位移关系      ⑤

得     ⑥

从小金属块滑至车中点C开始到小金属块停在车的左端的过程中，系统外力为零，动量守恒，设向右为正方向，且最后共同速度为     ⑦

得

由能量守恒有       ⑧

 得     ⑨

由⑥⑨得      ⑩

①~⑩每式2分