题目内容
如图所示，足够长的U型光滑金属导轨平面与水平面成
角，其中MN与PQ平行导轨间距为L， 导轨平面与磁感应强度为B的匀强磁场垂直，导轨电阻不计.金属捧a b由静止开始沿导轨下滑，并与两导轨始终保持垂直且良好接触，ab棒接入电路的电阻为R，当流过棒ab某一横截面的电量为q时。此时金属棒的速度大小为v，则金属棒ab在这一过程中
A．ab棒运动的平均速度大小为 |
B．此时金属棒的加速度为 |
C．此过程中产生的焦耳热为 |
D．金属棒ab沿轨道下滑的最大速度为 |
B
解析试题分析：根据牛顿第二定律，有：mgsinθ-BIL=ma；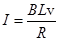
,所以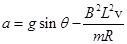
，B正确；从a的瞬时值表达式可以看出，随速度的增加，加速度减小，即金属板做加速度逐渐减小的变加速运动，平均速度不是 ,A错误；根据焦耳定律，
，其中的I为电流的有效值，而q=It中的I为电流的平均值，所以根据题目的已知量无法计算此过程中产生的焦耳热，C错误；当a=0时，速度最大
,D错误。
考点：本题考查了法拉第电磁感应定律和电磁感应的力学问题。
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
表示线框受到的安培力，P
表示线圈中的热功率，并以逆时针方向为感应电流正方向，向右为力的正方向，线圈在图示位置为位移起点，则下列图像中正确的是
一足够长的铜管竖直放置，将一截面与铜管的内截面相同、质量为m的永久磁铁块由管上端口放人管内，不考虑磁铁与铜管间的摩擦，磁铁的运动速度可能是（ ）
| A．逐渐增大到定值后保持不变 |
| B．逐渐增大到一定值时又开始碱小．然后又越来越大 |
| C．逐渐增大到一定值时又开始减小，到一定值后保持不变 |
| D．逐渐增大到一定值时又开始减小到一定值之后在一定区间变动 |
如图所示为演示自感现象实验的电路，实验时先闭合开关S，稳定后设通过线圈L的电流为I1，通过小灯泡A的电流为I2，小灯泡处于正常发光状态，迅速断开开关S，则可观察到灯泡A闪亮一下后熄灭，在灯泡A闪亮的短暂过程中，下列说法正确的是
| A．线圈L中电流I1逐渐减为零 |
| B．线圈L两端a端电势高于b端电势 |
| C．灯泡A中电流由I1逐渐减为零，方向与I2相反 |
| D．灯泡A中的电流I2逐渐减为零，方向不变 |