题目内容
19. 如图,竖直平面内的轨道Ⅰ和Ⅱ都由两段直杆连接而成,两轨道长度相等,一小球穿过细直杆且球与两轨道间的动摩擦因数相等.用相同的水平恒力将穿在轨道最低点B的静止小球,分别沿Ⅰ和Ⅱ推至最高点A,假定球在经过轨道转折点的前后速度大小不变.全过程中动能增量分别为△Ek1、△Ek2,重力势能增量分别为△EP1、△EP2,则( )
如图,竖直平面内的轨道Ⅰ和Ⅱ都由两段直杆连接而成,两轨道长度相等,一小球穿过细直杆且球与两轨道间的动摩擦因数相等.用相同的水平恒力将穿在轨道最低点B的静止小球,分别沿Ⅰ和Ⅱ推至最高点A,假定球在经过轨道转折点的前后速度大小不变.全过程中动能增量分别为△Ek1、△Ek2,重力势能增量分别为△EP1、△EP2,则( )| A. | △Ek1=△Ek2,△EP1=△EP2 | B. | △Ek1>△Ek2,△EP1=△EP2 | ||
| C. | △Ek1<△Ek2,△EP1=△EP2 | D. | △Ek1>△Ek2,△EP1<△EP2 |
分析 先分析整个过程摩擦力做功关系,根据动能定理比较动能的增加量;由重力做功情况,分析重力势能增量关系.
解答 解:设任一斜面的倾角为θ,斜面的长度为s,则物体在该斜面上下滑时摩擦力做功为 Wf=-Wf=-μ(mgcosθ+Fsinθ)•s=-μmgx-μFh,x是斜面底边的长度,h是斜面的高度,可知小球沿两轨道运动时,摩擦力做功相等,根据动能定理得:WF-mgh-Wf=△Ek,
知两次情况拉力做功相等,摩擦力做功相等,重力做功相等,则动能的变化量相等.即有△Ek1=△Ek2.
根据WG=mgh知,重力做功相等,则重力势能增量相等,即有△EP1=△EP2,故A正确.
故选:A
点评 本题考查了动能定理与运动学的综合,通过动能定理比较动能变化量的关系,关键要知道滑动摩擦力做功与水平位移有关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 发射月球探测卫星要经过多次变轨,如图Ⅰ是某月球探测卫星发射后的近地轨道,Ⅱ、Ⅲ是两次变轨后的转移轨道,O点是Ⅱ、Ⅲ轨道的近地点,Q、P分别是Ⅱ、Ⅲ轨道的远地点,则下列说法正确的是( )
发射月球探测卫星要经过多次变轨,如图Ⅰ是某月球探测卫星发射后的近地轨道,Ⅱ、Ⅲ是两次变轨后的转移轨道,O点是Ⅱ、Ⅲ轨道的近地点,Q、P分别是Ⅱ、Ⅲ轨道的远地点,则下列说法正确的是( )
 发射月球探测卫星要经过多次变轨,如图Ⅰ是某月球探测卫星发射后的近地轨道,Ⅱ、Ⅲ是两次变轨后的转移轨道,O点是Ⅱ、Ⅲ轨道的近地点,Q、P分别是Ⅱ、Ⅲ轨道的远地点,则下列说法正确的是( )
发射月球探测卫星要经过多次变轨,如图Ⅰ是某月球探测卫星发射后的近地轨道,Ⅱ、Ⅲ是两次变轨后的转移轨道,O点是Ⅱ、Ⅲ轨道的近地点,Q、P分别是Ⅱ、Ⅲ轨道的远地点,则下列说法正确的是( )| A. | 在三个轨道上卫星在O点的速度相同 | |
| B. | 在三个轨道上卫星在O点的加速度相同 | |
| C. | 卫星在Q点的机械能等于在P点的机械能 | |
| D. | 卫星在Q点的机械能大于在P点的机械能 |
10. 小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
 小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )
小文同学在探究物体做曲线运动的条件时,将一条形磁铁放在桌面的A位置,让小钢珠在水平桌面上以初速度v0运动,得到小钢珠的运动轨迹.图中a、b、c、d哪一条为其运动轨迹( )| A. | a | B. | b | C. | c | D. | d |
7.伽利略开创了实验研究和逻辑推理相结合探索自然规律的科学方法,利用这种方法伽利略发现的规律有( )
| A. | 物体之间普遍存在相互吸引力 | |
| B. | 力不是维持物体运动的原因 | |
| C. | 物体间的相互作用力总是大小相等、方向相反 | |
| D. | 忽略空气阻力,重物与轻物下落得同样快 |
14.下面哪一组单位属于国际单位制中的基本单位( )
| A. | N、kg、m | B. | m、kg、s | C. | kg、J、s | D. | m/s2、kg、J |
4.在物理学发展中,许多物理学家的科学研究推动了人类文明进程.对以下几位物理学家所做贡献的叙述中,符合史实的是( )
| A. | 卡文迪许发现了万有引力定律 | |
| B. | 亚里士多德通过理想实验提出力并不是维持物体运动的原因 | |
| C. | 库仑总结并确认了真空中两个静止点电荷之间的相互作用规律 | |
| D. | 牛顿应用“理想斜面实验”推翻了亚里士多德的“力是维持物体运动的原因”观点 |
11.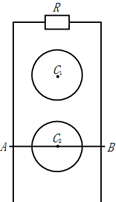 如图所示,竖直光滑导轨上端接入一定值电阻R,C1和C2是半径都为a的两圆形磁场区域,其区域内的磁场方向都垂直于导轨平面向外,区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,C2中磁场的磁感强度恒为B2,一质量为m、电阻为r、长度为L的金属杆AB穿过区域C2的圆心C2垂直地跨放在两导轨上,且与导轨接触良好,并恰能保存静止.则( )
如图所示,竖直光滑导轨上端接入一定值电阻R,C1和C2是半径都为a的两圆形磁场区域,其区域内的磁场方向都垂直于导轨平面向外,区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,C2中磁场的磁感强度恒为B2,一质量为m、电阻为r、长度为L的金属杆AB穿过区域C2的圆心C2垂直地跨放在两导轨上,且与导轨接触良好,并恰能保存静止.则( )
 如图所示,竖直光滑导轨上端接入一定值电阻R,C1和C2是半径都为a的两圆形磁场区域,其区域内的磁场方向都垂直于导轨平面向外,区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,C2中磁场的磁感强度恒为B2,一质量为m、电阻为r、长度为L的金属杆AB穿过区域C2的圆心C2垂直地跨放在两导轨上,且与导轨接触良好,并恰能保存静止.则( )
如图所示,竖直光滑导轨上端接入一定值电阻R,C1和C2是半径都为a的两圆形磁场区域,其区域内的磁场方向都垂直于导轨平面向外,区域C1中磁场的磁感强度随时间按B1=b+kt(k>0)变化,C2中磁场的磁感强度恒为B2,一质量为m、电阻为r、长度为L的金属杆AB穿过区域C2的圆心C2垂直地跨放在两导轨上,且与导轨接触良好,并恰能保存静止.则( )| A. | 通过金属杆的电流大小为$\frac{mg}{{B}_{2}L}$ | |
| B. | 通过金属杆的电流方向为从B到A | |
| C. | 定值电阻的阻值为R=$\frac{2πk{B}_{2}{a}^{3}}{mg}$-r | |
| D. | 整个电路中产生的热功率P=$\frac{πkamg}{2{B}_{2}}$ |
8.电场中等势面如图所示,下列关于该电场描述正确的是( )
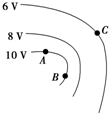

| A. | A点的电场强度比C点的小 | |
| B. | 电荷沿等势面AB移动的过程中,电场力始终不做功 | |
| C. | 负电荷在A点的电势能比在C点的电势能大 | |
| D. | 正电荷由A移动到C,电场力做负功 |
9.关于磁场和磁感线的描述,下列说法正确的是( )
| A. | 磁感线可以形象地描述磁场的强弱和方向,它每一点的切线方向表示该点的磁场方向 | |
| B. | 磁感线是从磁铁的N极指向S极 | |
| C. | 只有磁体才能产生磁场 | |
| D. | 磁感线就是磁场中碎铁屑排列成的曲线 |