题目内容
a、b、c、d是匀强电场中的四个点，它们正好是一个矩形的四个顶点．电场线与矩形所在平面平行．已知a点的电势为30V，b点的电势为36V，d点的电势为14V，如图，由此可知c点的电势为（ ）| A、14 V | B、20 V | C、24 V | D、30 V |
分析：在匀强电场中两点之间的电势差U=Edcosθ，所以Uba=Ucd据此解得c点的电势．
解答：解：根据在匀强电场中两点之间的电势差U=Edcosθ，设电场线与ba之间的夹角为θ，则电场线与cd之间的夹角也是θ，设ba=cd=L，则：
Uba=Ucd=ELcosθ
又：Uba=φb-φa=36V-30V=6V
所以：φc=Ucd+φd=6V+14V=20V
故选：B
Uba=Ucd=ELcosθ
又：Uba=φb-φa=36V-30V=6V
所以：φc=Ucd+φd=6V+14V=20V
故选：B
点评：①在匀强电场中将某一线段等分同时就将该线段两端的电势差等分；②在匀强电场中电场线平行且均匀分布故等势线平行且均匀分布．以上两点是解决此类题目的金钥匙．
练习册系列答案
相关题目
如果a、b、c、d是匀强电场中的四个点，它们正好是一个梯形的四个顶点，电场线与梯形所在的平面平行，ab平行cd，且ab边长为cd边长的一半，已知a点的电势是3V，b点的电势是5V，c点的电势是7V，由此可知，d点的电势为（ ）
（2007?浙江）a、b、c、d是匀强电场中的四个点，它们正好是一个矩形的四个顶点．电场线与矩形所在平面平行．已知a点的电势为20V，b点的电势为24V，d点的电势为4V，如图，由此可知c点的电势为（ ）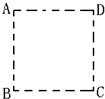
如图所示，A、B、C、D是匀强电场中一正方形的四个顶点．已知A、B、C三点的电势分别为UA=15V，UB=3V，UC=3V，由此可得D点的电势为UD=
a、b、c、d是匀强电场中的四个点，它们正好是一个矩形的四个顶点．电场线与矩形所在平面平行．已知a点的电势为20V，b点的电势为25V，d点的电势、c点的电势可能为（ ）
（2005?闵行区二模）本题中A．B分别为一期教材、二期新教材分叉题，考生选择只能选A组的全部或B组的全部完成．