题目内容
5. 如图所示是一种液体深度自动监测仪示意图,在容器的底部水平放置一平面镜,在平面镜上方有一光屏与平面镜平行.激光器发出的一束光以的入射角射到液面上,进入液体中的光线经平面镜反射后再从液体的上表面射出,打在光屏上形成一亮点,液体的深度变化后光屏上亮点向左移动了2$\sqrt{3}$dm,已知该液体折射率n=$\sqrt{3}$.真空中光速为c=3.0×108 m/s.不考虑经液面反射的光线.求:
如图所示是一种液体深度自动监测仪示意图,在容器的底部水平放置一平面镜,在平面镜上方有一光屏与平面镜平行.激光器发出的一束光以的入射角射到液面上,进入液体中的光线经平面镜反射后再从液体的上表面射出,打在光屏上形成一亮点,液体的深度变化后光屏上亮点向左移动了2$\sqrt{3}$dm,已知该液体折射率n=$\sqrt{3}$.真空中光速为c=3.0×108 m/s.不考虑经液面反射的光线.求:①液面高度的变化量;
②液面的深度变化前后激光从发出到打到光屏上的时间变化了多少?
分析 ①画出光路图,通过数学几何关系结合折射定律求出液面高度的变化量.
②根据v=$\frac{c}{n}$求出光在液体中传播的速度大小.分别求出光在液体深度变化前后在上升高度这段过程中运行的时间,从而求出时间的变化量.
解答 解:①光路图所示.设入射角为α,折射角为β,原来液面深度为h,液面深度增加△h,屏上光点移动的距离
s=2$\sqrt{3}$ dm
根据折射定律 n=$\frac{sinα}{sinβ}$得 β=30°
由几何关系得
2htanβ+2△htanα=2(△h+h)tanβ+s
得△h=$\frac{s}{2(tanα-tanβ)}$
代入解得△h=1.5dm
②光在该液体中的传播速度为 v=$\frac{c}{n}$=$\sqrt{3}$×108 m/s
液体的深度变化前后激光从发出到打到光屏上的时间变化为△t=$\frac{2△h}{vcosβ}$-$\frac{2△h}{ccosα}$=0
答:
①液面高度的变化量为1.5dm;
②液体的深度变化前后激光从发出到打到光屏上的时间变化了0.
点评 本题考查了几何光学问题,对数学几何能力要求较高,关键是作出光路图,通过折射定律以及速度与折射率的关系式进行求解.

练习册系列答案
相关题目
13. 家庭中用的取暖器,正常工作时所用电压是按照图中正弦规律变化的交流电,取暖器正常工作时的电流是3A.下列表述正确的是( )
家庭中用的取暖器,正常工作时所用电压是按照图中正弦规律变化的交流电,取暖器正常工作时的电流是3A.下列表述正确的是( )
 家庭中用的取暖器,正常工作时所用电压是按照图中正弦规律变化的交流电,取暖器正常工作时的电流是3A.下列表述正确的是( )
家庭中用的取暖器,正常工作时所用电压是按照图中正弦规律变化的交流电,取暖器正常工作时的电流是3A.下列表述正确的是( )| A. | 该交流电的有效值是220V | |
| B. | 该交流电的周期是0.01S | |
| C. | 该交流电的表达式为U=311sin100t(V) | |
| D. | 取暖器正常工作时的功率是880W |
10.据英国《卫报》网站2015年1月6日报道,在太阳系之外,科学家发现了一颗最适宜人类居住的类地行星,绕恒星橙矮星运行,命名为“开普勒438b”.假设该行星与地球绕恒星均做匀速圆周运动,其运行的周期为地球运行周期的p倍,橙矮星的质量为太阳的q倍. 则该行星与地球的( )
| A. | 轨道半径之比为 $\root{3}{pq}$ | B. | 轨道半径之比为$\root{3}{p^2}$ | ||
| C. | 线速度之比为$\root{3}{{\frac{q}{p}}}$ | D. | 线速度之比为$\sqrt{\frac{1}{p}}$ |
17.两个半径相同的金属小球,带电量之比为1:7,相距为r(可视为点电荷),两者相互接触后再放回原来的位置上,则相互作用力可能为原来的( )
| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{9}{7}$ | D. | $\frac{16}{7}$ |
14.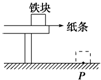 如图所示,一铁块压着一张纸条放在水平桌面上,当以较大速度v抽出纸条后,铁块掉在地上的P点,若以2v速度抽出纸条,则铁块落地点为( )
如图所示,一铁块压着一张纸条放在水平桌面上,当以较大速度v抽出纸条后,铁块掉在地上的P点,若以2v速度抽出纸条,则铁块落地点为( )
 如图所示,一铁块压着一张纸条放在水平桌面上,当以较大速度v抽出纸条后,铁块掉在地上的P点,若以2v速度抽出纸条,则铁块落地点为( )
如图所示,一铁块压着一张纸条放在水平桌面上,当以较大速度v抽出纸条后,铁块掉在地上的P点,若以2v速度抽出纸条,则铁块落地点为( )| A. | 仍在P点 | B. | 在P点左侧 | ||
| C. | 在P点右侧不远处 | D. | 在P点右侧原水平位移的两倍处 |
 如图所示,质量为m=2kg的直角劈形木块的顶角为θ=37°,被外力F顶靠在竖直墙上.已知木块与墙间的最大静摩擦力和木块对墙的压力成正比,即Ffm=kFN,比例系数为k=0.5,问垂直作用于BC边的外力F取何值时木块能保持静止状态?(取g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,质量为m=2kg的直角劈形木块的顶角为θ=37°,被外力F顶靠在竖直墙上.已知木块与墙间的最大静摩擦力和木块对墙的压力成正比,即Ffm=kFN,比例系数为k=0.5,问垂直作用于BC边的外力F取何值时木块能保持静止状态?(取g=10m/s2,sin37°=0.6,cos37°=0.8) 如图所示,物体m在倾角为α斜面A点(高为h)下滑,滑到C点静止,物体与斜面、平面的动摩擦因数均为μ,A、C间的水平距离为S.求物从A到C的过程中摩擦力做的总功?物体滑到斜面低端B点时,重力的瞬时功率?
如图所示,物体m在倾角为α斜面A点(高为h)下滑,滑到C点静止,物体与斜面、平面的动摩擦因数均为μ,A、C间的水平距离为S.求物从A到C的过程中摩擦力做的总功?物体滑到斜面低端B点时,重力的瞬时功率?