题目内容
 (2011?丰台区二模)如图所示,竖直平面内有四分之一圆弧轨道固定在水平桌面上,圆心为O点.一小滑块自圆弧轨道A处由静止开始自由滑下,在B点沿水平方向飞出,落到水平地面C点.已知小滑块的质量为m=1.0kg,C点与B点的水平距离为1.0m,B点高度为1.25m,圆弧轨道半径R=1.0m,取g=10m/s2.求小滑块:
(2011?丰台区二模)如图所示,竖直平面内有四分之一圆弧轨道固定在水平桌面上,圆心为O点.一小滑块自圆弧轨道A处由静止开始自由滑下,在B点沿水平方向飞出,落到水平地面C点.已知小滑块的质量为m=1.0kg,C点与B点的水平距离为1.0m,B点高度为1.25m,圆弧轨道半径R=1.0m,取g=10m/s2.求小滑块:(1)从B点飞出时的速度大小;
(2)在B点时对圆弧轨道的压力大小;
(3)沿圆弧轨道下滑过程中克服摩擦力所做的功.
分析:(1)滑块从B点飞出后做平抛运动,由高度和水平距离可求出平抛运动的初速度,即求得从B点飞出时的速度大小;
(2)滑块经过B点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律求出支持力,由牛顿第三定律得到滑块对轨道的压力.
(3)沿圆弧轨道下滑过程中重力和摩擦力做功,根据动能定理求解滑块克服摩擦力所做的功..
(2)滑块经过B点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律求出支持力,由牛顿第三定律得到滑块对轨道的压力.
(3)沿圆弧轨道下滑过程中重力和摩擦力做功,根据动能定理求解滑块克服摩擦力所做的功..
解答:解:(1)滑块从B点飞出后做平抛运动,设从B点飞出时的速度大小为v,则有
竖直方向:h=
gt2
水平方向:x=vt
解得 v=2m/s
(2)滑块经过B点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律得
N-mg=m
解得 N=14N
根据牛顿第三定律得,在B点时滑块对圆弧轨道的压力大小为N′=N=14N,方向竖直向下.
(3)设沿圆弧轨道下滑过程中滑块克服摩擦力所做的功为W,由动能定理得
mgR-W=
mv2
解得 W=8J
答:(1)从B点飞出时的速度大小为2m/s;
(2)在B点时对圆弧轨道的压力大小是14N;
(3)沿圆弧轨道下滑过程中克服摩擦力所做的功是8J.
竖直方向:h=
| 1 |
| 2 |
水平方向:x=vt
解得 v=2m/s
(2)滑块经过B点时,由重力和轨道的支持力的合力提供向心力,由牛顿第二定律得
N-mg=m
| v2 |
| R |
解得 N=14N
根据牛顿第三定律得,在B点时滑块对圆弧轨道的压力大小为N′=N=14N,方向竖直向下.
(3)设沿圆弧轨道下滑过程中滑块克服摩擦力所做的功为W,由动能定理得
mgR-W=
| 1 |
| 2 |
解得 W=8J
答:(1)从B点飞出时的速度大小为2m/s;
(2)在B点时对圆弧轨道的压力大小是14N;
(3)沿圆弧轨道下滑过程中克服摩擦力所做的功是8J.
点评:本题是平抛运动和动能定理的综合应用,速度是它们之间联系的纽带.根据动能定理求解变力做功是常用的思路.

练习册系列答案
相关题目
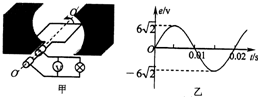 (2011?丰台区二模)如图甲所示为一台小型发电机构造的示意图,线圈逆时针转动,产生的电动势随时间变化的正弦规律图象如图乙所示.发电机线圈电阻为1.0Ω,外接灯泡的电阻为9.0Ω.则( )
(2011?丰台区二模)如图甲所示为一台小型发电机构造的示意图,线圈逆时针转动,产生的电动势随时间变化的正弦规律图象如图乙所示.发电机线圈电阻为1.0Ω,外接灯泡的电阻为9.0Ω.则( )