题目内容
【题目】如图所示，两根相同的轻质弹簧，中间与质量为m的圆环相连于O位置，另一端各自固定在同一水平线上的P、Q两点，弹簧恰好处于原长L，圆环套在粗糙的竖直细杆上，细杆上的A、B两点关于O点对称，OA=H．现将圆环沿杆拉至A位置由静止释放，当下滑到速度最大时，弹簧与细杆间的夹角为θ，整个过程中，弹簧处于弹性限度范围内．重力加速度为g．求：
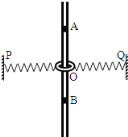
（1）圆环过O点时的加速度；
（2）圆环过B点的瞬时速度；
（3）每根轻质弹簧的劲度系数．
【答案】（1）a=g （2）
（3） 
【解析】
试题分析：（1）物体下落到O点时只受重力作用，由牛顿第二定律得：F=mg=ma （2分）
解得：a=g （2分）
（2）圆环从A到B过程中，有对称性可知，弹簧弹力做总功为零，圆环不受摩擦力作用， （2分）
只有重力做功，由动能定理得：
（2分）
解得： （1分）
（3）下落过程中，当环所受合力为零时速度最大 （1分）
由牛顿第二定律有： 
解得：
（2分）
由胡克定律得： 
（1分）
弹簧的伸长量为：
（2分）
解得： （1分）
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
相关题目
