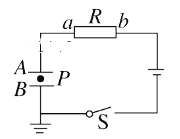
题目内容
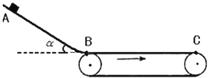
【题目】如图所示,一物体从高为![]() ,倾角
,倾角![]() 斜坡上的A点由静止开始下滑,经过B点后进入水平向右运动的传送带上
斜坡上的A点由静止开始下滑,经过B点后进入水平向右运动的传送带上![]() 设经过B点前后速度大小不变
设经过B点前后速度大小不变![]() ,物体与斜坡和传送带的动摩擦因数均为
,物体与斜坡和传送带的动摩擦因数均为![]() ,传送带长为10m,传送带匀速运动的速度为
,传送带长为10m,传送带匀速运动的速度为![]() 取
取![]() ,
,![]() ,
,![]() ,求:
,求:
![]() 物体到达B点时的速度。
物体到达B点时的速度。
![]() 物体从A点到C点离开传送带的时间。
物体从A点到C点离开传送带的时间。
【答案】(1)4m/s;(2)5.6s
【解析】
(1) 在斜坡上,物体重力,摩擦力,支持力,由牛顿第二定律可得:
mgsinα-f=ma1
在垂直斜面方向上:
FN=mgcosα
f=μFN
代入数据解得:a1=gsinα-μgcosα=10×0.6-0.25×10×0.8=4m/s2
又因为
h=x1sinα
![]()
vB=a1t1
代入数据解得:
![]()
![]()
vB=4×1m/s=4m/s;
(2) 当物体进入水平传送带上,由于速度大于传送带的速度,则物体先做匀减速运动,则:
a2=-μg=-2.5m/s2
由运动学可得:2a2x2=v2-vB2
v-vB=a2t2
代入数据解得:
![]()
![]()
因为x2<L,则物体先做匀减速运动,速度与传送带速度相等时,随后与传送带一起做匀速直线运动,则:
![]()
故物体从A点到C点离开传送带的时间为:
t=t1+t2+t3=1s+0.8s+3.8s=5.6s.。

练习册系列答案
相关题目