题目内容
5．
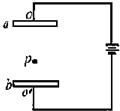如图所示，水平放置的平行金属板a、b分别与电源的两极相连，带电液滴P在金属板a、b间保持静止，现设法使P固定，减小两极板间的距离，然后释放P，则P在电场内将（ ）| A． | 沿水平方向做匀速直线运动 | B． | 竖直向上做加速运动 | ||
| C． | 竖直向下做加速运动 | D． | 仍然保持静止状态 |
分析 对带电液滴受力分析，判断出受到的电场力方向，当两板间距离变小时，场强增大，根据受力分析即可判断运动
解答 解：由于平行板与电源相连，故两极板间的电势差不变，
开始带电液滴静止，此时处于平衡状态，故mg=qE
当距离减小时，根据E=$\frac{U}{d}$可知，场强增大，带电液滴受到的电场力增大，故qE′＞mg，故带电液滴向上做加速运动，故B正确
故选：B
点评 本题主要考查了对带电液滴的受力分析，判断出距离变化后场强的变化即可
练习册系列答案
相关题目
15．
如图，一木块放在水平桌面上，在水平方向上共受到三个力即F1、F2和摩擦力作用，木块处于静止状态，其中F1=10N、F2=4N，若撤去力F1，则木块在水平方向受到的合力为（ ）
如图，一木块放在水平桌面上，在水平方向上共受到三个力即F1、F2和摩擦力作用，木块处于静止状态，其中F1=10N、F2=4N，若撤去力F1，则木块在水平方向受到的合力为（ ）| A． | 10N，方向向左 | B． | 6N，方向向右 | C． | 4N，方向向左 | D． | 零 |
16．实验室中准备了下列器材：
待测干电池（电动势约1.5V，内阻约1.0Ω）
电流表G（满偏电流1.5mA，内阻10Ω）
电流表A（量程0～0.60A，内阻约0.10Ω）
滑动变阻器R1（0～20Ω，2A）
滑动变阻器R2（0～100Ω，1A）
定值电阻R3=990Ω，开关S和导线若干
①小明同学选用上述器材（滑动变阻器只选用了一个）测定一节干电池的电动势和内阻．为了能较为准确地进行测量和操作方便，实验中选用的滑动变阻器，应是R1．（填代号）
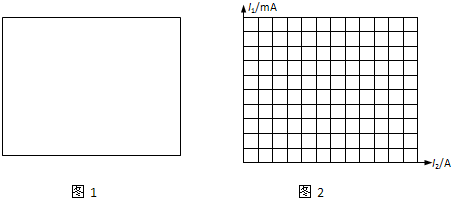
②请在图1方框中画出他的实验电路图．
③小明在实验得出的数据（I1为电流表G的示数，I2为电流表A的示数）如表，请在图2中作出的I1-I2图线，并由该图线求得：被测干电池的电动势E=1.46V，内阻r=0.76Ω．
待测干电池（电动势约1.5V，内阻约1.0Ω）
电流表G（满偏电流1.5mA，内阻10Ω）
电流表A（量程0～0.60A，内阻约0.10Ω）
滑动变阻器R1（0～20Ω，2A）
滑动变阻器R2（0～100Ω，1A）
定值电阻R3=990Ω，开关S和导线若干
①小明同学选用上述器材（滑动变阻器只选用了一个）测定一节干电池的电动势和内阻．为了能较为准确地进行测量和操作方便，实验中选用的滑动变阻器，应是R1．（填代号）
②请在图1方框中画出他的实验电路图．
③小明在实验得出的数据（I1为电流表G的示数，I2为电流表A的示数）如表，请在图2中作出的I1-I2图线，并由该图线求得：被测干电池的电动势E=1.46V，内阻r=0.76Ω．
| I2（A） | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| I1（mA） | 1.40 | 1.36 | 1.25 | 1.18 | 1.10 |
20．现要通过实验验证机械能守恒定律．实验装置如图1所示：水平桌面上固定一倾斜的气垫导轨；导轨上A点处有一带长方形遮光片的滑块，其总质量为M，左端由跨过轻质光滑定滑轮的细绳与一质量为m的砝码相连；遮光片两条长边与导轨垂直；导轨上B点有一光电门，可以测试遮光片经过光电门时的挡光时间t，用d表示A点到导轨低端C点的距离，h表示A与C的高度差，b表示遮光片的宽度，s表示A，B两点的距离，将遮光片通过光电门的平均速度看作滑块通过B点时的瞬时速度．用g表示重力加速度．
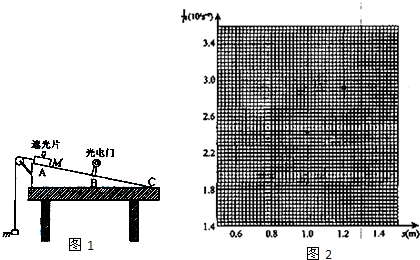
完成下列填空和作图；
（1）若将滑块自A点由静止释放，则在滑块从A运动至B的过程中，滑块、遮光片与砝码组成的系统重力势能的减小量可表示为Mg$\frac{h}{d}$s-mgs．动能的增加量可表示为$\frac{1}{2}$（m+M）$\frac{{b}^{2}}{{t}^{2}}$．若在运动过程中机械能守恒，$\frac{1}{{t}^{2}}$与s的关系式为$\frac{1}{{t}^{2}}$=$\frac{2（hM-dm）g}{（M+m）d{b}^{2}}$s．
（2）多次改变光电门的位置，每次均令滑块自同一点（A点）下滑，测量相应的s与t值，结果如表所示：
以s为横坐标，$\frac{1}{{t}^{2}}$为纵坐标，在图2坐标纸中描出第1和第5个数据点；根据5个数据点作直线，求得该直线的斜率k=2.39×104m-1•s-2 （保留3位有效数字）．
由测得的h、d、b、M和m数值可以计算出$\frac{1}{{t}^{2}}$-s直线的斜率k0，将k和k0进行比较，若其差值在实验允许的范围内，则可认为此实验验证了机械能守恒定律．
完成下列填空和作图；
（1）若将滑块自A点由静止释放，则在滑块从A运动至B的过程中，滑块、遮光片与砝码组成的系统重力势能的减小量可表示为Mg$\frac{h}{d}$s-mgs．动能的增加量可表示为$\frac{1}{2}$（m+M）$\frac{{b}^{2}}{{t}^{2}}$．若在运动过程中机械能守恒，$\frac{1}{{t}^{2}}$与s的关系式为$\frac{1}{{t}^{2}}$=$\frac{2（hM-dm）g}{（M+m）d{b}^{2}}$s．
（2）多次改变光电门的位置，每次均令滑块自同一点（A点）下滑，测量相应的s与t值，结果如表所示：
| 1 | 2 | 3 | 4 | 5 | |
| S（m） | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| T（m/s） | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| 1/t2（104s-2） | 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |
由测得的h、d、b、M和m数值可以计算出$\frac{1}{{t}^{2}}$-s直线的斜率k0，将k和k0进行比较，若其差值在实验允许的范围内，则可认为此实验验证了机械能守恒定律．
14．假设地球同步卫星的轨道半径是地球半径的n倍，则下列有关地球同步卫星的叙述正确的是（ ）
| A． | 运行速度是第一宇宙速度的$\frac{1}{n}$倍 | |
| B． | 运行速度是第一宇宙速度的$\sqrt{\frac{1}{n}}$倍 | |
| C． | 向心加速度是地球赤道上物体随地球自转的向心加速度的n倍 | |
| D． | 向心加速度是地球赤道上物体随地球自转的向心加速度的$\frac{1}{n}$倍 |
一艘宇宙飞船的总质量为M0，装有发动机推力显示仪、速度显示仪以及计时器．在外太空航行时遇到一个“漂浮”的小天体块，其体积大小和飞船差不多．宇航员决定采用动力学的方法估测它的质量．首先让飞船的船头慢慢和天体块“对接”，然后开动飞船发动机推动天体块一起匀加速直线运动（原理示意如图），从推力显示仪上读出此时飞船的推力恒为F，接下来，宇航员还需记录哪些数据才可以测出该天体块的质量？请用字母符号表示这些数据，求出小天体块的质量M的表达式．