题目内容
10. 如图所示,一个绝缘光滑半圆环轨道放在竖直向下的匀强电场E中,在半圆环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )
如图所示,一个绝缘光滑半圆环轨道放在竖直向下的匀强电场E中,在半圆环的上端,一个质量为m,带电量为+q的小球由静止开始沿轨道运动,则( )| A. | 小球运动过程中机械能守恒 | B. | 在最低点球对环的压力为mg | ||
| C. | 在最低点球对环的压力为3(mg+qE) | D. | 小球经过环的最低点时速度最大 |
分析 小球运动过程中电场力做功,机械能不守恒.根据动能定理知小球经过环的最低点时速度最大.根据动能定理求出小球经过在最低点时的速度,由牛顿第二定律求出环对球的支持力,得到球对环的压力.
解答 解:
A、小球运动过程中电场力做功,机械能不守恒.故A错误.
B、小球从最高点到最低点的过程,根据动能定理得:(mg+qE)R=$\frac{1}{2}m{v}^{2}$ 又由N-mg-qE=$\frac{m{v}^{2}}{R}$,联立解得N=3(mg+qE).故B错误,C正确.
小球从最高点到最低点的过程中,合力做正功,则根据动能定理得知,动能增加,速率增大,所以小球经过环的最低点时速度最大.故D正确.
故选:CD.
点评 本题是带电体在匀强电场中做圆周运动的问题,由动能定理和牛顿运动定律结合求解是常用的思路.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1.一辆汽车保持恒定速率驶过一座圆弧形拱桥,在此过程中( )

| A. | 汽车做匀速运动 | B. | 汽车做匀变速运动 | ||
| C. | 汽车所受合力不变 | D. | 汽车加速度大小恒定 |
18.长度为25m的铁链悬挂在天花板上的O点,放开铁链,让其自由下落,则铁链全部通过O点下方45m处的A点所用的时间为( )(g=10m/s2)
| A. | 1s | B. | 1.5s | C. | 2s | D. | 2.5s |
5.下列公式中定义的物理量不是采用比值定义法得出的是( )
| A. | E=$\frac{F}{q}$ | B. | R=ρ$\frac{I}{S}$ | C. | B=$\frac{F}{IL}$ | D. | C=$\frac{Q}{U}$ |
15. 如图所示,北京天安门广场警察统一装备了被称为“智能单警”的电力驱动单人车巡逻.该单人车是一种两轮式左右并行布置结构的具有自平衡系统的电动车,利用倒立摆控制原理,使车体始终保持“平衡”.若警察质量为M,电动车质量为m,当警察驾驶电动车在水平地面上匀加速前进时(不计空气阻力),下列说法正确的是( )
如图所示,北京天安门广场警察统一装备了被称为“智能单警”的电力驱动单人车巡逻.该单人车是一种两轮式左右并行布置结构的具有自平衡系统的电动车,利用倒立摆控制原理,使车体始终保持“平衡”.若警察质量为M,电动车质量为m,当警察驾驶电动车在水平地面上匀加速前进时(不计空气阻力),下列说法正确的是( )
 如图所示,北京天安门广场警察统一装备了被称为“智能单警”的电力驱动单人车巡逻.该单人车是一种两轮式左右并行布置结构的具有自平衡系统的电动车,利用倒立摆控制原理,使车体始终保持“平衡”.若警察质量为M,电动车质量为m,当警察驾驶电动车在水平地面上匀加速前进时(不计空气阻力),下列说法正确的是( )
如图所示,北京天安门广场警察统一装备了被称为“智能单警”的电力驱动单人车巡逻.该单人车是一种两轮式左右并行布置结构的具有自平衡系统的电动车,利用倒立摆控制原理,使车体始终保持“平衡”.若警察质量为M,电动车质量为m,当警察驾驶电动车在水平地面上匀加速前进时(不计空气阻力),下列说法正确的是( )| A. | 电动车牵引力逐渐增大 | B. | 电动车对警察作用力方向竖直向上 | ||
| C. | 地面受到的压力大小为(M+m)g | D. | 警察对电动车作用力大小为Mg |
16. 物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是( )
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是( )
 物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是( )
物理学中有些问题的结论不一定必须通过计算才能验证,有时只需通过一定的分析就可以判断结论是否正确.如图所示为两个彼此平行且共轴的半径分别为R1和R2的圆环,两圆环上的电荷量均为q(q>0),而且电荷均匀分布.两圆环的圆心O1和O2相距为2a,联线的中点为O,轴线上的A点在O点右侧与O点相距为r(r<a).试分析判断下列关于A点处电场强度大小E的表达式(式中k为静电力常量)正确的是( )| A. | E=|$\frac{kq{R}_{1}}{{[R}_{1}^{2}+(a+r)^{2}]}$-$\frac{kq{R}_{2}}{[{R}_{2}^{2}+(a-r)^{2}]}$| | |
| B. | E=|$\frac{kq{R}_{1}}{[{{R}_{1}}^{2}+(a+r)^{2}]^{\frac{3}{2}}}$-$\frac{kq{R}_{2}}{[{R}_{2}^{2}+(a-r)^{2}]^{\frac{3}{2}}}$] | |
| C. | E=|$\frac{kq(a+r)}{{[R}_{1}^{2}+(a+r)^{2}]}$-$\frac{kq(a-r)}{[{R}_{2}^{2}+(a-r)^{2}]}$| | |
| D. | E=|$\frac{kq(a+r)}{[{R}_{1}^{2}+(a+r)^{2}]^{\frac{3}{2}}}$-$\frac{kq(a-r)}{[{R}_{2}^{2}+(a-r)^{2}]^{\frac{3}{2}}}$| |
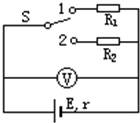 在图所示的电路中,电源的内阻不能忽略.已知定值电阻R1=9Ω,R2=4Ω.当单刀双掷开关S置于位置1时,电压表读数为2.7V.则当S置于位置2时,电压表读数为2.4V.求:电源的电动势E和内阻r.
在图所示的电路中,电源的内阻不能忽略.已知定值电阻R1=9Ω,R2=4Ω.当单刀双掷开关S置于位置1时,电压表读数为2.7V.则当S置于位置2时,电压表读数为2.4V.求:电源的电动势E和内阻r.