题目内容
验证“机械能守恒定律”的实验采用重物自由下落的方法(g=9.8m/s2):
(1)通过验证
mυ2=mgh来验证机械能守恒定律时,对纸带上起点的要求是
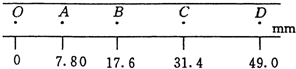
(2)若实验中所用重锤质量m=1kg,打点纸带如图所示,打点时间间隔为0.02s,则记录B点时,重锤的速度υB=
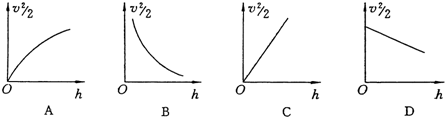
(3)根据纸带算出相关各点的速度υ,量出下落距离h,则以
为纵轴,画出的图象应是图中的
(1)通过验证
| 1 |
| 2 |
初速度等于零
初速度等于零
;为此,所选择纸带的第一、二两点间距应接近2mm
2mm
.(2)若实验中所用重锤质量m=1kg,打点纸带如图所示,打点时间间隔为0.02s,则记录B点时,重锤的速度υB=
0.59m/s
0.59m/s
,重锤动能EkB=0.174J
0.174J
.从开始下落起至B点,重锤的重力势能减少量是0.173J
0.173J
,因此可得出的结论是:在误差允许范围内,重物下落的机械能守恒.
在误差允许范围内,重物下落的机械能守恒.
.
(3)根据纸带算出相关各点的速度υ,量出下落距离h,则以
| υ2 |
| 2 |
C
C
,图线的斜率表示g
g
.
分析:书本上的实验,我们要从实验原理、实验仪器、实验步骤、实验数据处理、实验注意事项这几点去搞清楚.
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答:解:(1)用公式
mυ2=mgh来验证机械能守恒定律时,对纸带上起点的要求是重锤是从初速度为零开始,
打点计时器的打点频率为50 Hz,打点周期为0.02 s,重物开始下落后,在第一个打点周期内重物下落的高度所以所选的纸带最初两点间的距离接近2mm,
h=
gT2=
9.8×0.022 m≈2 mm.
(2)利用匀变速直线运动的推论
vB=
=0.59m/s,
重锤的动能EKB=
mvB2=0.174J
从开始下落至B点,重锤的重力势能减少量△Ep=mgh=1×9.8×0.176J=0.173J.
得出的结论是在误差允许范围内,重物下落的机械能守恒.
(3)利用
-h图线处理数据,如果mgh=
mv2那么图线应该是过原点的直线,斜率就等于g.
故选C
故答案为:(1)初速度等于零,2mm
(2)0.59m/s 0.174J 0.173J
在误差允许范围内,重物下落的机械能守恒.
(3)C g
| 1 |
| 2 |
打点计时器的打点频率为50 Hz,打点周期为0.02 s,重物开始下落后,在第一个打点周期内重物下落的高度所以所选的纸带最初两点间的距离接近2mm,
h=
| 1 |
| 2 |
| 1 |
| 2 |
(2)利用匀变速直线运动的推论
vB=
| xAC |
| 2T |
重锤的动能EKB=
| 1 |
| 2 |
从开始下落至B点,重锤的重力势能减少量△Ep=mgh=1×9.8×0.176J=0.173J.
得出的结论是在误差允许范围内,重物下落的机械能守恒.
(3)利用
| υ2 |
| 2 |
| 1 |
| 2 |
故选C
故答案为:(1)初速度等于零,2mm
(2)0.59m/s 0.174J 0.173J
在误差允许范围内,重物下落的机械能守恒.
(3)C g
点评:利用图象问题结合数学知识处理物理数据是实验研究常用的方法.我们更多的研究直线图形,找出其直线的斜率和截距.

练习册系列答案
相关题目
 在用打点计时器验证机械能守恒定律的实验中,使质量为m=1kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一点,当地的重力加速度为g=9.80m/s2.那么:
在用打点计时器验证机械能守恒定律的实验中,使质量为m=1kg的重物自由下落,打点计时器在纸带上打出一系列的点,选取一条符合实验要求的纸带如图所示.O为第一个点,A、B、C为从合适位置开始选取的三个连续点(其他点未画出).已知打点计时器每隔0.02s打一点,当地的重力加速度为g=9.80m/s2.那么: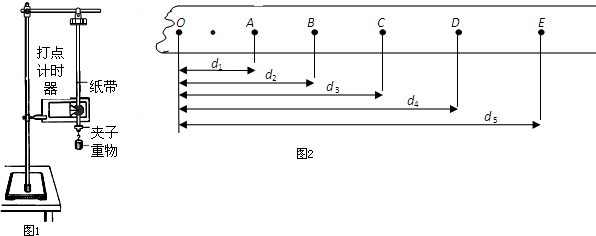
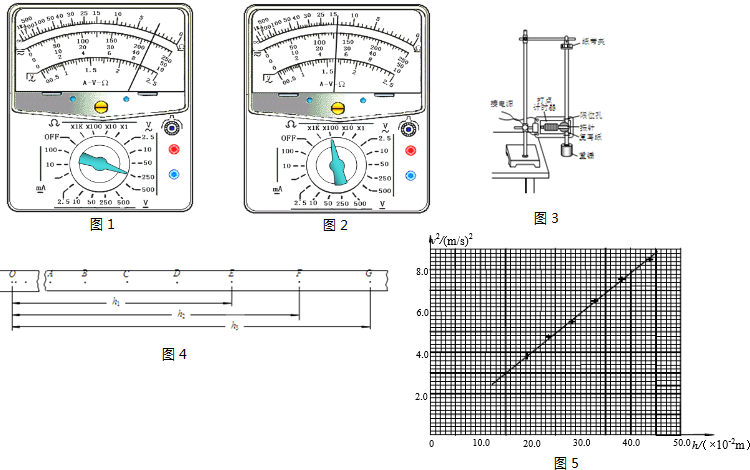
 (1)在《验证机械能守恒定律》的实验中,打点计时器所用电源为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg,甲、乙、丙三学生分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.18cm、0.19cm、0.25cm,从纸带中可看出
(1)在《验证机械能守恒定律》的实验中,打点计时器所用电源为50Hz,当地重力加速度的值为9.80m/s2,测得所用重物的质量为1.00kg,甲、乙、丙三学生分别用同一装置打出三条纸带,量出各纸带上第1、2两点间的距离分别为0.18cm、0.19cm、0.25cm,从纸带中可看出