题目内容
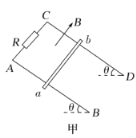
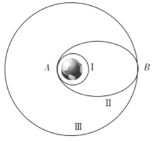
【题目】如图所示，在竖直平面内半径为R的四分之一圆弧轨道AB、水平轨道BC与斜面轨道CD平滑连接在一起（轨道为光滑凹槽），斜面轨道足够长。在圆弧轨道上静止着N个半径为r（rR）的完全相同小球，小球恰好将圆弧轨道铺满，从最高点A到最低点B依次标记为1、2、3……N。现将圆弧轨道末端B处的阻挡物拿走，N个小球由静止开始沿轨道运动，不计摩擦与空气阻力，下列说法正确的是（ ）
A.N个小球在运动过程中始终不会散开
B.第N个小球在斜面上能达到的最大高度为R
C.如果斜面倾角为45°，小球不可以全部到达斜面上
D.第1个小球到达最低点的速度
【答案】ACD
【解析】
A．在AB段，后面的小球总要往前推前面的小球，在BC水平段，各小球保持匀速运动，相互之间仅仅接触，但无弹力作用，在CD段，前面的小球会减速运动，后面的小球速度比它大，因此又将推着它向前运动，所以整个运动过程中小球始终不会散开，A正确；
B．在AB段时，高度在
之上的小球只占总数的
，而在斜面上各小球连成直线铺开，根据机械能守恒定律可知第N个小球在斜面上能达到的最大高度小于R，B错误；
CD．同样对整体在AB段时，重心低于，所以第1个小球到达最低点的速度
，C错误；D正确。
故选D。
练习册系列答案
相关题目
