题目内容
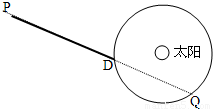 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
【答案】分析:设一年时间为T,则三个月的时间为 T,三个月时间地球绕太阳转过90°角,若地球到太阳的距离为r,则由几何关系得DQ=
T,三个月时间地球绕太阳转过90°角,若地球到太阳的距离为r,则由几何关系得DQ=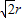 ,飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,根据位移公式求出半径,根据万有引力公式即可求得地球与太阳间的万有引力大小.
,飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,根据位移公式求出半径,根据万有引力公式即可求得地球与太阳间的万有引力大小.
解答:解:设一年时间为T,则三个月的时间为 T,三个月时间地球绕太阳转过90°角,
T,三个月时间地球绕太阳转过90°角,
若地球到太阳的距离为r,则由几何关系得DQ=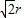
a=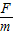 而DQ=PQ-PD=
而DQ=PQ-PD=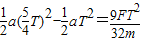
解得:r=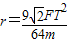
故所求F引 =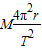 =
=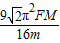
答:地球与太阳间的万有引力大小为=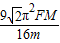
点评:本题主要考查了万有引力公式及匀变速直线运动位移时间公式的应用,并结合几何关系求解,难度适中.
 T,三个月时间地球绕太阳转过90°角,若地球到太阳的距离为r,则由几何关系得DQ=
T,三个月时间地球绕太阳转过90°角,若地球到太阳的距离为r,则由几何关系得DQ=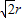 ,飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,根据位移公式求出半径,根据万有引力公式即可求得地球与太阳间的万有引力大小.
,飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,根据位移公式求出半径,根据万有引力公式即可求得地球与太阳间的万有引力大小.解答:解:设一年时间为T,则三个月的时间为
 T,三个月时间地球绕太阳转过90°角,
T,三个月时间地球绕太阳转过90°角,若地球到太阳的距离为r,则由几何关系得DQ=
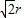
a=
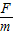 而DQ=PQ-PD=
而DQ=PQ-PD=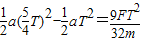
解得:r=
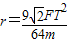
故所求F引 =
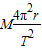 =
=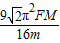
答:地球与太阳间的万有引力大小为=
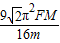
点评:本题主要考查了万有引力公式及匀变速直线运动位移时间公式的应用,并结合几何关系求解,难度适中.

练习册系列答案
相关题目
 (2007?深圳一模)设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
(2007?深圳一模)设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)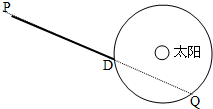
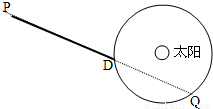 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)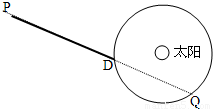 设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)
设地球的质量为M且绕太阳做匀速圆周运动,有一质量为m的飞船由静止开始从P点在恒力F的作用下沿PD方向做匀加速直线运动,一年后在D点飞船掠过地球上空,再过三个月,飞船在Q处掠过地球上空,如图所示,根据以上条件,求地球与太阳间的万有引力大小. (设太阳与地球的万有引力作用不改变飞船所受恒力F的大小和方向,飞船到地球表面的距离远小于地球与太阳间的距离)