题目内容
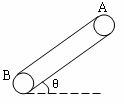
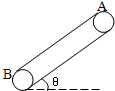如图，传送带与水平面夹角θ=37°，并以v=l0m/s的速度运行，在传送带的A端轻轻地放一小物体，若已知传送带与物体之间的动摩擦因数μ=0.5，传送带A到B端的距离s=l6m，则小物体从A端运动到B端所需的时间可能是（g=10m/s2）
- A.1.8s
- B.2.0s
- C.2．ls
- D.4.0s
BD
分析：（1）若传送带顺时针运动，对物体受力分析，根据物体的受力的情况求得物体的加速度的大小，根据运动学的规律可以求得物体运动的时间．
（2）传送带沿逆时针方向转动时，物体的受到的摩擦力的方向会发生变化，根据摩擦力变化前和变化后的不同的受力，求出加速度的大小，再计算运动的时间即可．
解答：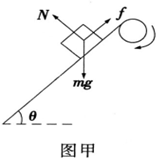
解：若传送带顺时针运动，对放在传送带上的小物体进行受力分析，
小物体沿传送带向下滑动时，无论传送带时静止还是沿顺时针分析正常转动，小物体的受力情况完全一样，
都是在垂直传送带的方向受力平衡，受到沿传送带向上的滑动摩擦力，
如图甲所示，
根据牛顿第二定律，小物体沿传送带下滑的加速度为：
a1=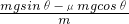
=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s2=2m/s2，
小物体从A端运动到B端做初速度为零的匀加速直线运动，设需要的时间为t，则
s=
a1t2，
t=
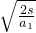=4s
（3）当传送带沿逆时针方向正常转动时，开始时，传送带作用于小物体的摩擦力沿传送带向下，
小物体下滑的加速度a2=g（sinθ+μcosθ）=10m/s2
小物体加速到与传送带运行速度相同是需要的时间为
t1=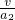
=
s=1s，
在这段时间内，小物体沿传送带下滑的距离为s1=at2=×10×1=5m
由于 μ＜tanθ，
此后，小物体沿传送带继续加速下滑时，它相对于传送带的运动的方向向下，
因此传送带对小物体的摩擦力方向有改为沿传送带向上，
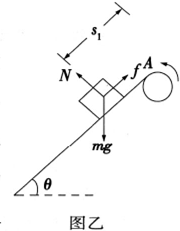如图乙所示，
其加速度变为a1=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s2=2m/s2
小物体从该位置起运动到B端的位移为s-s1=16m-5m=11m
小物体做初速度为v=10m/s、加速度为a1的匀加速直线运动，
由s-s1=vt2-a1t22
代入数据，解得t2=1s（t2=-11s舍去）
所以，小物体从A端运动到B端的时间为t=t1+t2=2s．
故选BD
点评：本题中最容易出错的地方在传送带逆时针运动的计算，物体受到的摩擦力的方向是变化的，从而导致物体的运动的加速度不同，物体运动的情况也就不同，根据前后两种不同的运动计算时间即可．
分析：（1）若传送带顺时针运动，对物体受力分析，根据物体的受力的情况求得物体的加速度的大小，根据运动学的规律可以求得物体运动的时间．
（2）传送带沿逆时针方向转动时，物体的受到的摩擦力的方向会发生变化，根据摩擦力变化前和变化后的不同的受力，求出加速度的大小，再计算运动的时间即可．
解答：
解：若传送带顺时针运动，对放在传送带上的小物体进行受力分析，小物体沿传送带向下滑动时，无论传送带时静止还是沿顺时针分析正常转动，小物体的受力情况完全一样，
都是在垂直传送带的方向受力平衡，受到沿传送带向上的滑动摩擦力，
如图甲所示，
根据牛顿第二定律，小物体沿传送带下滑的加速度为：
a1=
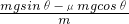=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s2=2m/s2，小物体从A端运动到B端做初速度为零的匀加速直线运动，设需要的时间为t，则
s=
a1t2，t=
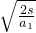=4s（3）当传送带沿逆时针方向正常转动时，开始时，传送带作用于小物体的摩擦力沿传送带向下，
小物体下滑的加速度a2=g（sinθ+μcosθ）=10m/s2
小物体加速到与传送带运行速度相同是需要的时间为
t1=
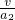=s=1s，在这段时间内，小物体沿传送带下滑的距离为s1=
at2=×10×1=5m由于 μ＜tanθ，
此后，小物体沿传送带继续加速下滑时，它相对于传送带的运动的方向向下，
因此传送带对小物体的摩擦力方向有改为沿传送带向上，
如图乙所示，其加速度变为a1=g（sinθ-μcosθ）=10×（0.6-0.5×0.8）m/s2=2m/s2
小物体从该位置起运动到B端的位移为s-s1=16m-5m=11m
小物体做初速度为v=10m/s、加速度为a1的匀加速直线运动，
由s-s1=vt2-
a1t22代入数据，解得t2=1s（t2=-11s舍去）
所以，小物体从A端运动到B端的时间为t=t1+t2=2s．
故选BD
点评：本题中最容易出错的地方在传送带逆时针运动的计算，物体受到的摩擦力的方向是变化的，从而导致物体的运动的加速度不同，物体运动的情况也就不同，根据前后两种不同的运动计算时间即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
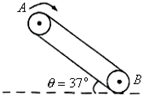传送带与水平面夹角37°，皮带以10m/s的速率运动，皮带轮沿顺时针方向转动，如图所示．今在传送带上端A处无初速地放上一个质量为m=0.5kg的小物块，它与传送带间的动摩擦因数为0.5，若传送带A到B的长度为16m，g取10m/s2，则物体从A运动到B的时间为多少？
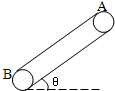如图，传送带与水平面夹角θ=37°，并以v=l0m/s的速度运行，在传送带的A端轻轻地放一小物体，若已知传送带与物体之间的动摩擦因数μ=0.5，传送带A到B端的距离s=l6m，则小物体从A端运动到B端所需的时间可能是（g=10m/s2）（ ）
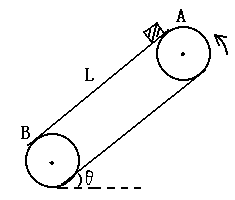轻放一质量m=2千克的物块，它与传送带间的摩擦系数μ=0．5。若两轮间传送带的长度L=29米。（g取10米/秒2， sin37°=0．6，cos37°=0．8）求：（1）物块从传送带上端A运动到 B处所用时间和到B处时的速度大小。（2）物块从传送带上端A运动到 B处的过程中摩擦力对物块所做的功。(3) 物块从传送带上端A运动到 B处的过程中物块和传送带所产生的总热量。 