题目内容
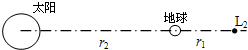 已知太阳质量为m1,地球质量为m2,月球半径为r,月球表面重力加速度为g.
已知太阳质量为m1,地球质量为m2,月球半径为r,月球表面重力加速度为g.(1)若探月卫星“嫦娥二号”绕月球做圆周运动的周期为T,求“嫦娥二号”距月面的高度.
(2)若太阳与地球系统的拉格朗日L2点与地球中心之间的距离为r1,太阳中心与地球中心之间的距离为r2,如示所示.2011年8月,我国第二颗月球探测卫星“嫦娥二号”在完成探月任务后,受控精确进入拉格朗日L2点的环绕轨道.估算在拉格朗日L2点,太阳对“嫦娥二号”的引力与地球对“嫦娥二号”的引力之比.
分析:(1)由万有引力提供向心力列出等式,在月面根据万有引力等于重力列出等式求解
(2)根据万有引力定律表示出太阳对嫦娥二号的引力和地球对嫦娥二号的引力进行求解
(2)根据万有引力定律表示出太阳对嫦娥二号的引力和地球对嫦娥二号的引力进行求解
解答:解:(1)设月球质量为m3,“嫦娥二号”质量为m,由万有引力提供向心力,
有:G
=m(r+h)(
)2,
而在月面:G
=mg
解得:h=
-r
(2)太阳对嫦娥二号的引力为F1=G
,
地球对嫦娥二号的引力为F2=G
,
所以两力之比为
答:(1)“嫦娥二号”距月面的高度是
-r
(2)太阳对“嫦娥二号”的引力与地球对“嫦娥二号”的引力之比是
有:G
| m3m |
| (r+h)2 |
| 2π |
| T |
而在月面:G
| m3m |
| r2 |
解得:h=
| 3 |
| ||
(2)太阳对嫦娥二号的引力为F1=G
| m1m |
| (r1+r2)2 |
地球对嫦娥二号的引力为F2=G
| m2m |
| r12 |
所以两力之比为
m1
| ||
| m2(r1+r2)2 |
答:(1)“嫦娥二号”距月面的高度是
| 3 |
| ||
(2)太阳对“嫦娥二号”的引力与地球对“嫦娥二号”的引力之比是
m1
| ||
| m2(r1+r2)2 |
点评:解决本题的关键掌握万有引力提供向心力公式,要注意黄金代换式的应用,难度适中.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
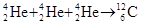 ,到那时太阳向外辐射的能量是由上述两种核反应共同产生.若已知
,到那时太阳向外辐射的能量是由上述两种核反应共同产生.若已知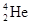 的质量为m1,
的质量为m1, 的质量为m2,则下列判断正确的是
的质量为m2,则下列判断正确的是 