题目内容
8. 边长为a的正方形处于有界磁场中,如图所示.两个电子分别以速度VA和VC水平射入匀强磁场后,分别从A处和C处射出,则VA:VC=1:2,粒子在磁场中经历的时间之比tA:tC=2:1.
边长为a的正方形处于有界磁场中,如图所示.两个电子分别以速度VA和VC水平射入匀强磁场后,分别从A处和C处射出,则VA:VC=1:2,粒子在磁场中经历的时间之比tA:tC=2:1.
分析 由几何关系可知从两孔射出的粒子的运动半径,则由洛仑兹力充当向心力可得出粒子的速度关系;由周期公式及转过的角度可求得时间之比;由向心力公式可求得加速度之比.
解答 解:电子从C点射出,A为圆心,Rc=L,圆心角θc=$\frac{π}{2}$由R=$\frac{mv}{qB}$,
得vc=$\frac{eBL}{m}$运动时间为四分之一周期,即:${t}_{c}=\frac{1}{4}T=\frac{πm}{2eB}$
电子从A点射出,OA中点为圆心,RA=$\frac{L}{2}$,圆心角θd=π,
所以vA=$\frac{eBL}{2m}$,tA=${t}_{A}=\frac{1}{2}T=\frac{πm}{eB}$
由于运动的周期与速度无关,是相等的,
故vA:vC=1:2,tA:tC=2:1,
故答案为:1:2,2:1
点评 本题为带电粒子在磁场中运动的基本问题,只需根据题意明确粒子的运动半径及圆心即可顺利求解.

练习册系列答案
相关题目
18. 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
 如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )
如图所示,在匀速转动的电动机带动下,足够长的水平传送带以恒定速率V1匀速向右运动.一质量为m的滑块从传送带右端以水平向左的速率V2(V2>V1)滑上传送带,最终滑块又返回至传送带的右端.就上述过程,下列判断正确的有( )| A. | 滑块返回传送带右端时的速率为V2 | |
| B. | 此过程中传送带对滑块做功为$\frac{1}{2}$mv22-$\frac{1}{2}$mv12 | |
| C. | 此过程中滑块与传送带间摩擦产生的热量为 m(v1+v2)2 | |
| D. | 此过程中电动机做功为mv1(v1+v2) |
20. 如右图所示,A、B是被绝缘支架分别架起的相同金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
如右图所示,A、B是被绝缘支架分别架起的相同金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
 如右图所示,A、B是被绝缘支架分别架起的相同金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )
如右图所示,A、B是被绝缘支架分别架起的相同金属球,并相隔一定距离,其中A带正电,B不带电,则以下说法中正确的是( )| A. | 导体B带负电 | |
| B. | 导体B左端出现负电荷,右端出现正电荷,并且电荷量大小相等 | |
| C. | AB之间作用力是互相吸引 | |
| D. | 若A、B接触一下,A、B金属体所带总电荷量减少. |
17. 如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
 如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )
如图,质量为m的物体P放在光滑的倾角为θ的斜面体上,同时用力F向右推斜面体,使P与斜面体保持相对静止,在前进水平位移为S的过程中,斜面体对P做功为( )| A. | FS | B. | $\frac{(mgSsinθ)}{2}$ | C. | mgScosθ | D. | mgStanθ |
20.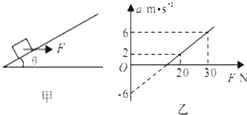 如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息能计算出( )
如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息能计算出( )
 如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息能计算出( )
如图甲所示.用一水平外力F拉着一个静止在倾角为θ的光滑斜面上的物体.逐渐增大F,物体做变加速运动,其加速度a随外力F变化的图象如图乙所示,若重力加速度g取10m/s2,根据图乙中所提供的信息能计算出( )| A. | 斜面的倾角 | |
| B. | 加速度为2m•s-2时物体所受的合外力 | |
| C. | 物体静止在斜面上所施加的最小外力 | |
| D. | 加速度为4m•s-2时物体的速度 |
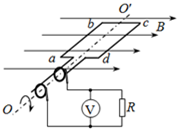 如图所示,abcd是交流发电机的矩形线圈,其面积为0.01m2,匝数n=100匝,线圈电阻r=2Ω,外电阻R=8Ω.线圈在磁感强度B=$\frac{2}{π}$T的匀强磁场中绕垂直于磁场的转轴OO′匀速转动,角速度ω=10πrad/s.求:
如图所示,abcd是交流发电机的矩形线圈,其面积为0.01m2,匝数n=100匝,线圈电阻r=2Ω,外电阻R=8Ω.线圈在磁感强度B=$\frac{2}{π}$T的匀强磁场中绕垂直于磁场的转轴OO′匀速转动,角速度ω=10πrad/s.求: 有四盏灯,接入如图所示的电路中.L1和L2都标有“220V,100W”,L3和L4都标有“220V,40W”.把电路接通后,最亮的灯将是( )
有四盏灯,接入如图所示的电路中.L1和L2都标有“220V,100W”,L3和L4都标有“220V,40W”.把电路接通后,最亮的灯将是( )