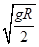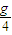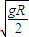题目内容
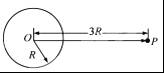
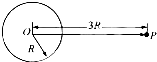如图所示，地球球心为O，半径为R，表面的重力加速度为g，一宇宙飞船绕地球无动力飞行且做椭圆轨道运动（椭圆轨道未画出）．轨道上P点距地心最远，距离为3R，为研究方便，假设地球不自转且忽略空气阻力，则（ ）分析：飞船在P点的加速度即为万有引力加速度，根据万有引力加速度的表达式可知加速度的大小与距球心的距离平方成反比，从而求出P点的加速度与地球表面重力加速的大小关系；根据椭圆轨道上卫星运动从远地点开始将做近心运动，满足万有引力大于运动所需要的向心力，从而确定线速度的大小关系．
解答：解：在地球表面重力加速度与万有引力加速度相等，根据牛顿第二定律有：
G
=ma?万有引力加速度a=
所以在地球表面有：
g=
P点的加速度ap=
=
=
=
g
故A正确B错误；
在椭圆轨道上飞船从P点开始将做近心运动，此时满足万有引力大于P点所需向心力即：
map＞m
如果飞船在P点绕地球做圆周运动时满足map=m
?v=
=
=
由此分析知：vp＜
所以C、D均错误．
故选：A
G
| mM |
| r2 |
| GM |
| r2 |
所以在地球表面有：
g=
| GM |
| R |
P点的加速度ap=
| GM |
| r2 |
| GM |
| (3R)2 |
| 1 |
| 9 |
| GM |
| R2 |
| 1 |
| 9 |
故A正确B错误；
在椭圆轨道上飞船从P点开始将做近心运动，此时满足万有引力大于P点所需向心力即：
map＞m
| ||
| 3R |
如果飞船在P点绕地球做圆周运动时满足map=m
| v2 |
| 3R |
| 3Rap |
3R×
|
|
由此分析知：vp＜
|
所以C、D均错误．
故选：A
点评：解决本题的关键掌握万有引力提供向心力和万有引力等于重力这两个理论，并能熟练运用．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
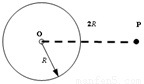
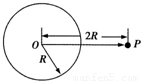
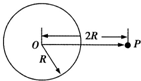如图所示，地球球心为O，半径为R，表面能重力加速度为g．一宇宙飞船绕地球无动力飞行且做椭圆运动，恰好经过距地心2R的P点，为研究方便，假设地球不自转且表面没有空气，则（ ）
