题目内容
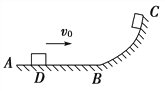
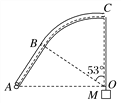
【题目】如图所示，光滑管状轨道ABC由直轨道AB和圆弧轨道BC组成，二者在B处相切并平滑连接，O为圆心，O、A在同一条水平线上，OC竖直，一直径略小于圆管直径的质量为m的小球，用细线穿过管道与质量为M的物块连接，将小球由A点静止释放，当小球运动到B处时细线断裂，小球继续运动。已知弧形轨道的半径为R＝
m，所对应的圆心角为53°，sin53°＝0.8，cos53°＝0.6，g＝10 m/s2.
(1)若M＝5m，求小球在直轨道部分运动时的加速度大小。
(2)若M＝5m，求小球从C点抛出后下落高度h＝
m时到C点的水平位移。
(3)M、m满足什么关系时，小球能够运动到C点？
【答案】（1）7m/s2
（2）
（3）
【解析】（1）设细线中张力为F，对小球：F-mgsin53°=ma
对物块：Mg-F=Ma
联立解得：a=7m/s2
（2）在Rt△OAB中，得： 
；
由v2=2axAB代入数据解得：v=2
m/s；
从B到C，根据机械能守恒，有： 
小球离开C后做平抛运动，有：
x=vCt 
联立并代入数据解得： 
（3）小球A→B：M、m系统机械能守恒，有： 
线断后，小球B→C， 
联立，解得： 
．
练习册系列答案
名校课堂系列答案
相关题目
