题目内容
2011年11月26日23时2分,好奇号火星探测器发射成功,顺利进入飞往火星的轨道,围绕火星环绕36周,于2012年8月6日成功降落在火星表面.假设着陆前,质量为m的火星探测器在接近火星表面的运动轨道视为运动,已知火星的质量为M,火星的半径为R,火星表面的重力加速度为g,引力常量为G,不考虑火星自转的影响,则火星探测器的( )
A、线速度v=
| ||||
B、角速度ω=
| ||||
C、运行周期T=2π
| ||||
D、向心加速度a=
|
分析:火星探测器在接近火星表面的运动轨道运动,由火星的万有引力提供向心力,重力等于万有引力,列式求解.
解答:解:火星探测器在接近火星表面的运动轨道运动,由火星的万有引力提供向心力,则得:
G
=m
═ma
则得线速度 v=
,向心加速度 a=
又由重力等于万有引力,得:mg=mω2R=m
R,得角速度ω=
,周期T=2π
,故AC正确,BD错误.
故选:AC
G
| Mm |
| R2 |
| v2 |
| R |
则得线速度 v=
|
| GM |
| R2 |
又由重力等于万有引力,得:mg=mω2R=m
| 4π2 |
| T2 |
|
|
故选:AC
点评:对于卫星类型,关键要掌握这两条思路:万有引力等于向心力,重力等于万有引力.

练习册系列答案
相关题目
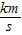 .
.