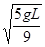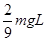题目内容
汽车与路面的动摩擦因数为μ,公路某转弯处半径为R(设最大静摩擦力等于滑动摩擦力),问:
(1)若路面水平,汽车转弯不发生侧滑,对汽车最大速度为多少?
(2)若将公路转弯处路面设计成外侧高、内侧低,使路面与水平面倾角为α,则汽车以多大速度转弯,可以使车与路面间无摩擦力?
(1)若路面水平,汽车转弯不发生侧滑,对汽车最大速度为多少?
(2)若将公路转弯处路面设计成外侧高、内侧低,使路面与水平面倾角为α,则汽车以多大速度转弯,可以使车与路面间无摩擦力?
(1) (2)
(2)
 (2)
(2)
解:(1)汽车在水平路面上转弯时,汽车转弯的向心力由静摩擦力提供,当静摩擦力达到最大时,汽车的转弯速度最大。由牛顿第二定律得:
 ?
?
 mg=m
mg=m (3分)
(3分)
解得 v1= (1分)
(1分)
(2) 当重力和支持力的合力恰提供向心力时,车与路面间无摩擦力,
则有
mg tanα=m (3分)
(3分)
解得 v2= (1分)
(1分)
本题考查圆周运动生活实例,要求汽车拐弯最大速度,必须弄清楚汽车拐弯时向心力来源,当重力和支持力的合力恰提供向心力时,车与路面间无摩擦力根据受力分析结合牛顿运动定律可得。
 ?
? mg=m
mg=m (3分)
(3分)解得 v1=
 (1分)
(1分)(2) 当重力和支持力的合力恰提供向心力时,车与路面间无摩擦力,
则有
mg tanα=m
 (3分)
(3分)解得 v2=
 (1分)
(1分)本题考查圆周运动生活实例,要求汽车拐弯最大速度,必须弄清楚汽车拐弯时向心力来源,当重力和支持力的合力恰提供向心力时,车与路面间无摩擦力根据受力分析结合牛顿运动定律可得。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目



 ,当圆台匀速旋转时A、B、C均没有滑动,则下列说法正确的是:( )
,当圆台匀速旋转时A、B、C均没有滑动,则下列说法正确的是:( )