题目内容
13. 质量M=2kg的长木板A(厚度可忽略)长度L=4m,在水平面上静止,用向右的水平恒力F=11N,使其加速到v0=1m/s,这时将质量m=1kg的木块B(木块大小可忽略),轻放在长木板的右端,从此时计时,经时间t1木块到达木板左端离开木板,此时将F撤去,从撤去F后再经过时间t2木块静止.已知木板与地面间的动摩擦因数为μ1=0.2,木块与木板间摩擦因数μ2=0.1,最大静摩擦力等于滑动摩擦力.(g=10m/s2),求:
质量M=2kg的长木板A(厚度可忽略)长度L=4m,在水平面上静止,用向右的水平恒力F=11N,使其加速到v0=1m/s,这时将质量m=1kg的木块B(木块大小可忽略),轻放在长木板的右端,从此时计时,经时间t1木块到达木板左端离开木板,此时将F撤去,从撤去F后再经过时间t2木块静止.已知木板与地面间的动摩擦因数为μ1=0.2,木块与木板间摩擦因数μ2=0.1,最大静摩擦力等于滑动摩擦力.(g=10m/s2),求:(1)从放上木块到木块离开木板的时间;
(2)木块在水平面上刚静止时距木板左端的距离S?
分析 (1)根据牛顿第二定律分别求出求出物块和木板的加速度大小,结合位移时间公式,抓住位移之差等于L求出木块放上木板到离开的时间.
(2)根据速度时间公式求出木块和木板在木块离开时的速度大小,结合速度时间公式求出木块速度减为零的时间,以及求出木块速度减为零的位移,结合木板的位移,求出木块在水平面上刚静止时距木板左端的距离.
解答 解:(1)物块B放上木板后,木块的加速度为:${a}_{1}={μ}_{2}g=1m/{s}^{2}$,
木板A的加速度为:${a}_{2}=\frac{F-{μ}_{2}mg-{μ}_{1}(M+m)g}{M}$=$\frac{11-0.1×10-0.2×30}{2}m/{s}^{2}$=2m/s2.
根据${v}_{0}t+\frac{1}{2}{a}_{2}{t}^{2}-\frac{1}{2}{a}_{1}{t}^{2}=L$代入数据解得:t=2s.
(2)物块离开木板时的速度为:v1=a1t=1×2m/s=2m/s,
木板的速度为:v2=v0+a2t=1+2×2m/s=5m/s,
木块做匀减速运动的加速度大小为:${a}_{3}={μ}_{1}g=2m/{s}^{2}$,
则木块速度减为零的时间为:${t}_{2}=\frac{{v}_{1}}{{a}_{3}}=\frac{2}{2}s=1s$,
木块的位移为:$x=\frac{{{v}_{1}}^{2}}{2{a}_{3}}=\frac{4}{4}m=1m$,
木板做匀减速运动的加速度大小也为2m/s2,则木板的位移为:
$x′={v}_{2}{t}_{2}-\frac{1}{2}{a}_{3}{{t}_{2}}^{2}=5×1-\frac{1}{2}×2×1$m=4m,
则木块水平面上静止时,距离木板左端的距离为:S=x′-x=4-1m=3m.
答:(1)从放上木块到木块离开木板的时间为2s;
(2)木块在水平面上刚静止时距木板左端的距离S为3m.
点评 解决本题的关键理清木块和木板在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案 如图所示,实线为一列横波某时刻的图象,这列波的传播速度为0.25m/s,经过时间1s后的波形为虚线所示.那么这列波的传播方向与在这段时间内质点P(x=0.1m处)所通过的路程是( )
如图所示,实线为一列横波某时刻的图象,这列波的传播速度为0.25m/s,经过时间1s后的波形为虚线所示.那么这列波的传播方向与在这段时间内质点P(x=0.1m处)所通过的路程是( )| A. | 向左,10 cm | B. | 向右,30 cm | C. | 向左,50 cm | D. | 向右,70 cm |
| A. | 光由空气射入玻璃时速度变慢,波长变短 | |
| B. | 光从玻璃射入空气发生全反射时,红光的临界角小于蓝光的临界角 | |
| C. | 光学镜头上的增透膜是利用光的干涉现象 | |
| D. | 在岸边观察前方水中的一条鱼,鱼的实际深度比看到的要浅 | |
| E. | 经过同一双缝所得干涉条纹,红光条纹宽度大于绿光条纹宽度 |
 如图所示,理想变压器n1=n2,n3=n4,n1:n3=55:1,所提供电压为正弦交变电压.现将各线圈做如下连接,正确的是( )
如图所示,理想变压器n1=n2,n3=n4,n1:n3=55:1,所提供电压为正弦交变电压.现将各线圈做如下连接,正确的是( )| A. | bc相接,从ad输入电压220V,NP相接,则MQ间电压为4V | |
| B. | ac相接,bd相接,从ad输入电压220V,则彼此独立的MN和PQ间电压都是4V | |
| C. | bc相接,从ad输入电压220V,MP相接,NQ相接,则MQ间电压为4V | |
| D. | ac相接,bd相接,从ad输入电压220V,MP相接,NQ相接,则MQ间电压为2V |
 如图所示,质量为m的小球(可视为质点)用长为L的细线悬挂于O点,自由静止在A位置.现用水平力F缓慢地将小球从A拉到B位置而静止,细线与竖直方向夹角为θ=60°,此时细线的拉力为F1,然后放手让小球从静止返回,到A点时细线的拉力为F2,则( )
如图所示,质量为m的小球(可视为质点)用长为L的细线悬挂于O点,自由静止在A位置.现用水平力F缓慢地将小球从A拉到B位置而静止,细线与竖直方向夹角为θ=60°,此时细线的拉力为F1,然后放手让小球从静止返回,到A点时细线的拉力为F2,则( )| A. | F1=F2=2mg | |
| B. | 从A到B,拉力F做功为F1L | |
| C. | 从B到A的过程中,小球受到的合外力大小不变 | |
| D. | 从B到A的过程中,小球重力的瞬时功率一直增大 |
 如图1,一单匝矩形金属线圈,其平面垂直于磁场放置,现让磁场按如图2所示正弦函数规律变化,则下面说法中正确的是( )
如图1,一单匝矩形金属线圈,其平面垂直于磁场放置,现让磁场按如图2所示正弦函数规律变化,则下面说法中正确的是( )| A. | t1时刻通过线圈的磁通量的绝对值最大,E感最小 | |
| B. | t2时刻通过线圈的磁通量变化率的绝对值最大;E感方向正在改变 | |
| C. | t3时刻通过线圈的磁通量的绝对值最大,E感大小为零 | |
| D. | 每当E感转换方向时,通过线圈的磁通量都是零 |
| A. | a、b、c三点的角速度相同 | B. | a、b两点的线速度相同 | ||
| C. | b、c两点的线速度相同 | D. | b、c两点的轨道半径相同 |
 如图所示,直线MN表示一条平直公路,甲、乙两辆汽车原来停在A、B两处,A、B间的距离为85m,现甲车先开始向右做匀加速直线运动,加速度a1=2.5m/s2,甲车运动6.0s时,乙车立即开始向右匀加速直线运动,加速度a2=5.0m/s2,求:
如图所示,直线MN表示一条平直公路,甲、乙两辆汽车原来停在A、B两处,A、B间的距离为85m,现甲车先开始向右做匀加速直线运动,加速度a1=2.5m/s2,甲车运动6.0s时,乙车立即开始向右匀加速直线运动,加速度a2=5.0m/s2,求: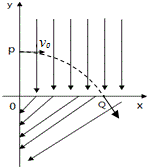 如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求:
如图所示,在空间建立平面直角坐标系,在第一象限内加上电场强度大小为E、方向沿-y轴方向的匀强电场,第四象限内加上电场强度大小也为E,方向与-x轴方向成某一夹角的匀强电场.现有一质量为m、带电荷量+q的不计重力的微粒自y轴上某点P开始以初速度v0沿+x轴方向进入第一象限,微粒通过坐标为(+x0,0)的Q点后以和第四象限内的电场垂直的方向进入第四象限,不计空气阻力.求: