题目内容
6. 蹦床运动员在空中运动时可视为质点,可依据装在弹性网上的传感器描绘出运动员对弹性网的压力随时间的F-t图象,试估算出运动员跃起的最大高度为(g取10m/s2)( )
蹦床运动员在空中运动时可视为质点,可依据装在弹性网上的传感器描绘出运动员对弹性网的压力随时间的F-t图象,试估算出运动员跃起的最大高度为(g取10m/s2)( )| A. | 1.5m | B. | 1.8m | C. | 5.0m | D. | 7.2m |
分析 运动员离开弹性网后做竖直上抛运动,图中压力传感器示数为零的时间即是运动员在空中运动的时间,根据平抛运动的对称性可知,运动员竖直上抛或自由下落的时间为空中时间的一半,据此可求出运动员跃起是最大高度.
解答 解:由图可知运动员在空中的最长时间为:t=4.3s-2.3s=2s
运动员做竖直上抛运动,所以跃起最大高度为:$h=\frac{1}{2}g(\frac{t}{2})^{2}$
将t=2s带入得:h=$\frac{1}{2}×10×(\frac{2}{2})^{2}$m=5m,故ABD错误,C正确.
故选:C.
点评 竖直上抛运动的对称性特点,是对竖直上抛运动考查的重点,要熟练掌握和应用竖直上抛运动的相关知识是解决本题的基础.

练习册系列答案
相关题目
16.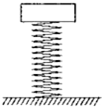 如图所示,一轻质弹簧的下端固定在水平面上,弹簧处于原长状态,若在其上端轻放一个质量为m的物体甲(物体与弹簧不连接,重力加速度为g),当甲下降高度为h时,其速度恰好变为零.若在轻弹簧上端轻放一质量为2m的物体乙,当乙下降高度h时,下列说法正确的是( )
如图所示,一轻质弹簧的下端固定在水平面上,弹簧处于原长状态,若在其上端轻放一个质量为m的物体甲(物体与弹簧不连接,重力加速度为g),当甲下降高度为h时,其速度恰好变为零.若在轻弹簧上端轻放一质量为2m的物体乙,当乙下降高度h时,下列说法正确的是( )
 如图所示,一轻质弹簧的下端固定在水平面上,弹簧处于原长状态,若在其上端轻放一个质量为m的物体甲(物体与弹簧不连接,重力加速度为g),当甲下降高度为h时,其速度恰好变为零.若在轻弹簧上端轻放一质量为2m的物体乙,当乙下降高度h时,下列说法正确的是( )
如图所示,一轻质弹簧的下端固定在水平面上,弹簧处于原长状态,若在其上端轻放一个质量为m的物体甲(物体与弹簧不连接,重力加速度为g),当甲下降高度为h时,其速度恰好变为零.若在轻弹簧上端轻放一质量为2m的物体乙,当乙下降高度h时,下列说法正确的是( )| A. | 乙速度也恰好为零 | |
| B. | 乙下降到h过程中乙的机械能先增大后减小 | |
| C. | 乙下降到h过程中乙与弹簧、地面组成的系统总势能一直增大 | |
| D. | 乙速度大小为$\sqrt{gh}$ |
14. 如图所示,电源电动势为E,内阻为r,电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小),电压表为理想表,当电键S闭合时,电容器C中一带电微粒恰好处于静止状态,有关下列说法中正确的是( )
如图所示,电源电动势为E,内阻为r,电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小),电压表为理想表,当电键S闭合时,电容器C中一带电微粒恰好处于静止状态,有关下列说法中正确的是( )
 如图所示,电源电动势为E,内阻为r,电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小),电压表为理想表,当电键S闭合时,电容器C中一带电微粒恰好处于静止状态,有关下列说法中正确的是( )
如图所示,电源电动势为E,内阻为r,电路中的R2、R3分别为总阻值一定的滑动变阻器,R0为定值电阻,R1为光敏电阻(其电阻随光照强度增大而减小),电压表为理想表,当电键S闭合时,电容器C中一带电微粒恰好处于静止状态,有关下列说法中正确的是( )| A. | 只逐渐增大R1的光照强度的过程中,电阻R0消耗的电功率变大,电阻R3中有向上的电流 | |
| B. | 只调节电阻R3的滑动端P2向上移动的过程中,电源消耗的功率变大,R3中有向上的电流 | |
| C. | 若断开电键S,电容器C所带电荷量不变,带电微粒仍然处于静止状态 | |
| D. | 只调节电阻R2的滑动端P1向下移动的过程中,电压表示数不变,带电微粒将向上运动 |
1.在如图所示的四种电场中,分别标记有a、b两点,下列说法正确的是( )
| A. | 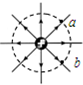 图中与点电荷等距的a、b两点电势相等 | |
| B. | 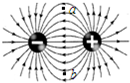 图中两等量异种电荷连线中垂线上与连线等距的a、b两点场强和电势都都相等 | |
| C. | 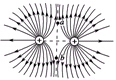 图中两等量同种电荷连线的中垂线与连线等距的a、b电势和场强都相等 | |
| D. |  图中匀强电场中的a、b两点电势和场强都相等 |
11.把一条电阻为16Ω,的均匀电阻丝截成等长的n段后,再并联起来,电阻变为1Ω,则n等于( )
| A. | 4 | B. | 2 | C. | 12 | D. | 8 |
18. 两光滑斜面放置在地面上,倾角分别为30°和45°、质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放.对于两次实验,下面结论中错误的是( )
两光滑斜面放置在地面上,倾角分别为30°和45°、质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放.对于两次实验,下面结论中错误的是( )
 两光滑斜面放置在地面上,倾角分别为30°和45°、质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放.对于两次实验,下面结论中错误的是( )
两光滑斜面放置在地面上,倾角分别为30°和45°、质量分别为2m和m的两个滑块用不可伸长的轻绳通过滑轮连接(不计滑轮的质量和摩擦),分别置于两个斜面上并由静止释放;若交换两滑块位置,再由静止释放.对于两次实验,下面结论中错误的是( )| A. | 滑块下滑加速度变大了 | B. | 绳子的拉力变小了 | ||
| C. | 地面对斜面的摩擦力大小不变 | D. | 地面对斜面的支持力变大了 |
15. 如图所示,半径为R、质量为m且分布均匀的闭合金属圆环用长为L的丝线悬挂于天花板下,其下方横放着一根通电直导线,今将环拉至摆线与竖直方向成q角的位置,无初速释放,设环在摆动过程中始终保持与导线在同一平面内,则( )
如图所示,半径为R、质量为m且分布均匀的闭合金属圆环用长为L的丝线悬挂于天花板下,其下方横放着一根通电直导线,今将环拉至摆线与竖直方向成q角的位置,无初速释放,设环在摆动过程中始终保持与导线在同一平面内,则( )
 如图所示,半径为R、质量为m且分布均匀的闭合金属圆环用长为L的丝线悬挂于天花板下,其下方横放着一根通电直导线,今将环拉至摆线与竖直方向成q角的位置,无初速释放,设环在摆动过程中始终保持与导线在同一平面内,则( )
如图所示,半径为R、质量为m且分布均匀的闭合金属圆环用长为L的丝线悬挂于天花板下,其下方横放着一根通电直导线,今将环拉至摆线与竖直方向成q角的位置,无初速释放,设环在摆动过程中始终保持与导线在同一平面内,则( )| A. | 环能摆到右侧同一高度处 | |
| B. | 环第一次摆到右边最高点过程中感应电流方向不变 | |
| C. | 环运动中所受安培力始终与速度方向相反 | |
| D. | 环运动中所受安培力始终沿竖直方向 |
16.关于滑动摩擦力,下列说法正确的是( )
| A. | 两物体间有滑动摩擦力,两物体间就一定有弹力 | |
| B. | 两物体间有滑动摩擦力,两物体就一定都是运动的 | |
| C. | 两物体都在运动且相互间存在弹力,则两物体间就一定有滑动摩擦力 | |
| D. | 两物体间有相对运动,两物体间就一定有滑动摩擦力 |
 如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,设向右为正方向,则关于A物体运动的加速度a、速度v、位移x及B对A的摩擦力Ff随时间变化的关系图象正确的是( )
如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,设向右为正方向,则关于A物体运动的加速度a、速度v、位移x及B对A的摩擦力Ff随时间变化的关系图象正确的是( )


