题目内容
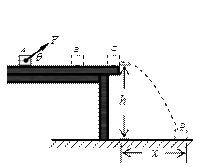
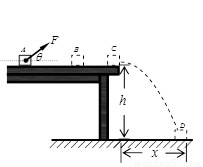
如图所示,水平台高h=0.8m,台上A点放有一大小可忽略的滑块,质量m=0.5kg,滑块与台面间的动摩擦因数μ=0.5;现对滑块施加一个斜向上的拉力F=5N,θ=37°,经t1=1s,滑块到达平台上B点时撤去拉力,滑块继续运动,最终落到地面上的D点,x=0.4m.(取sin37°=0.6,cos37°=0.8,g=10m/s2)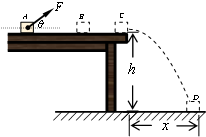
(1)求滑块在C点离开台面瞬间的速度;
(2)滑块在AB段的加速度大小;
(3)求AC间的距离.

(1)求滑块在C点离开台面瞬间的速度;
(2)滑块在AB段的加速度大小;
(3)求AC间的距离.
分析:(1)滑块在C点离开台面后做平抛运动,运用运动的分解法求解平抛运动的初速度,即为滑块在C点离开台面瞬间的速度;
(2)分析物体在AB段受力情况,根据牛顿第二定律求出加速度大小.
(3)由运动学公式求出AB段的位移大小和运动到B时滑块的速度,由动能定理求出BC间的距离,再求解AC间距离.
(2)分析物体在AB段受力情况,根据牛顿第二定律求出加速度大小.
(3)由运动学公式求出AB段的位移大小和运动到B时滑块的速度,由动能定理求出BC间的距离,再求解AC间距离.
解答: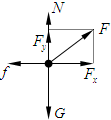 解:(1)在CD段,由平抛规律:
解:(1)在CD段,由平抛规律:
水平方向:x=vCtCD
竖直方向:h=
g
则滑块在C点离开台面瞬间的速度为
vC=
=
=1(m/s)
(2)在AB段,滑块受力如图
Fx=Fcosθ=4(N),Fy=Fsinθ=3(N)
N=mg-Fy=2(N)
f=μN=1(N)
滑块的加速度a=
=
=6(m/s2)
(3)由运动学规律得
xAB=
a
=
×6×12=3(m)
vB=a
=6×1=6(m/s)
在BC段,由动能定理-μmgxBC=
m
-
m
xBC=
=
=3.5m
AC间的距离
xAC=xAB+xBC=3+3.5=6.5(m)
答:
(1)滑块在C点离开台面瞬间的速度为1m/s.
(2)滑块在AB段的加速度大小为6m/s2;
(3)AC间的距离为6.5m.
 解:(1)在CD段,由平抛规律:
解:(1)在CD段,由平抛规律:水平方向:x=vCtCD
竖直方向:h=
| 1 |
| 2 |
| t | 2 CD |
则滑块在C点离开台面瞬间的速度为
vC=
| x | ||||
|
| 0.4 | ||||
|
(2)在AB段,滑块受力如图
Fx=Fcosθ=4(N),Fy=Fsinθ=3(N)
N=mg-Fy=2(N)
f=μN=1(N)
滑块的加速度a=
| Fx-f |
| m |
| 4-1 |
| 0.5 |
(3)由运动学规律得
xAB=
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
vB=a
| t | 1 |
在BC段,由动能定理-μmgxBC=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
xBC=
| ||||
| 2μg |
| 62-12 |
| 2×0.5×10 |
AC间的距离
xAC=xAB+xBC=3+3.5=6.5(m)
答:
(1)滑块在C点离开台面瞬间的速度为1m/s.
(2)滑块在AB段的加速度大小为6m/s2;
(3)AC间的距离为6.5m.
点评:本题是多过程问题,要抓住三个过程之间的速度关系、位移关系.考查综合应用动能定理、平抛运动、牛顿定律和运动学公式解决复杂物理问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目