题目内容
17.氢原子基态能量E1=-13.6eV,电子绕核做圆周运动的半径r1=0.53×10-10m.求氢原子处于n=4激发态时:(已知能量关系En=$\frac{1}{{n}^{2}}$E1,半径关系rn=n2r1,静电力常量k=9.0×109N•m2/C2)(1)原子系统具有的能量;
(2)电子在n=4轨道上运动的动能;
(3)要使n=4激发态的电子电离,至少要用多大频率的光照射?
分析 根据能量关系En=$\frac{1}{{n}^{2}}$E1,求出氢原子处于n=4激发态,原子系统所具有的能量.
根据库仑引力提供向心力得出电子在轨道n=4上运动的动能.
从n=4向n=1跃迁,能级差最大,发出的光子频率最大.
解答 解:(1)根据能量关系En=$\frac{1}{{n}^{2}}$E1,则有:E4=$\frac{{E}_{1}}{{4}^{2}}$=$\frac{-13.6}{16}$=-0.85eV
(2)因为r4=42r1
根据库仑引力提供向心力得:K$\frac{{e}^{2}}{{r}_{4}^{2}}$=m$\frac{{v}^{2}}{{r}_{4}}$
所以,EK4=$\frac{1}{2}$mv2=$\frac{K{e}^{2}}{32{r}_{1}}$=$\frac{9×1{0}^{9}×(1.6×1{0}^{-19})^{2}}{32×0.53×1{0}^{-10}}$J=0.85eV.
(3)要使n=4激发态的电子电离,据玻尔理论得,发出光子的能量为:
hγ=E1$\frac{1}{{4}^{2}}$;
解得:γ=$\frac{13.6×1.6×1{0}^{-19}}{16×6.63×1{0}^{-34}}$=2.1×1014 Hz.
答:(1)原子系统具有的能量为-0.85eV.
(2)电子在n=4轨道上运动的动能为0.85eV;
(3)要使n=4激发态的电子电离,至少要用2.1×1014 Hz频率的光照射.
点评 原子系统具有能量等于电子动能和系统具有的电势能之和.知道电子绕核旋转,靠库仑引力提供向心力.
考查对玻尔理论的理解和应用能力,关键抓住辐射的光子能量与能级差之间的关系.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
7.如图甲所示,为测定物体冲上粗糙斜面能达到的最大位移x与斜面倾角θ的关系,将某一物体每次以不变的初速率v0沿足够长的斜面向上推出,调节斜面与水平方向的夹角θ,实验测得x与斜面倾角θ的关系如图乙所示,g取10m/s2,根据图象可求出( )
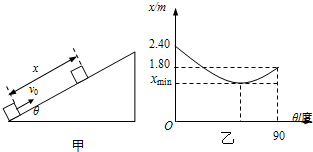

| A. | 物体的初速率6m/s,与斜面间的动摩擦因数μ=0.75 | |
| B. | 当θ=45°时,物体到最高点后将静止在斜面上 | |
| C. | 当θ=45°时,物体在斜面上滑行的位移x最小 | |
| D. | 物体在斜面上能达到的位移x的最小值为xmin=1.44m |
5.三个大小相等互成120度角的力F1=F2=F3=F,它们合成后合力大小是( )
| A. | 0 | B. | F | C. | 2F | D. | 3F |
2.以下说法正确的是( )
| A. | 哥白尼提出了“地心说” | |
| B. | 被命名为“笔尖下发现的行星”是天王星 | |
| C. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了“放大法” | |
| D. | 经典力学适用于宏观物体的运动,量子力学适用于微观粒子的运动 |
9.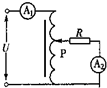 如图为一自耦变压器,它的特点是铁芯上只绕有一个线圈,把整个线圈作为原线圈,而取线圈的一部分作为副线圈.已知原线圈所接的正弦交流电电压为U,交流电流表A1、A2均为理想电流表,当触头P向上移动时,两个交流电流表的读数变化情况为( )
如图为一自耦变压器,它的特点是铁芯上只绕有一个线圈,把整个线圈作为原线圈,而取线圈的一部分作为副线圈.已知原线圈所接的正弦交流电电压为U,交流电流表A1、A2均为理想电流表,当触头P向上移动时,两个交流电流表的读数变化情况为( )
 如图为一自耦变压器,它的特点是铁芯上只绕有一个线圈,把整个线圈作为原线圈,而取线圈的一部分作为副线圈.已知原线圈所接的正弦交流电电压为U,交流电流表A1、A2均为理想电流表,当触头P向上移动时,两个交流电流表的读数变化情况为( )
如图为一自耦变压器,它的特点是铁芯上只绕有一个线圈,把整个线圈作为原线圈,而取线圈的一部分作为副线圈.已知原线圈所接的正弦交流电电压为U,交流电流表A1、A2均为理想电流表,当触头P向上移动时,两个交流电流表的读数变化情况为( )| A. | A1读数变小 | B. | A1读数不变 | C. | A2读数变大 | D. | A2读数变小 |
6.如图是某种正弦式交变电压的波形图,由图可确定该电压的( )
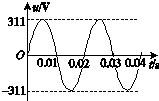

| A. | 周期是0.01 s | B. | 最大值是622 V | ||
| C. | 有效值是220 V | D. | 表达式为u=220sin 100πt(V) |

 如图所示,质量为m的木块置于斜面上,木块与斜面间的动摩擦因数为μ,在外力作用下,斜面以加速度a沿水平方向向右做匀加速运动,运动中物体m与斜面体相对静止.则木块受到的重力不做功,受到的支持力做负功,受到的摩擦力做正功(填“正功”,“负功”或“不做功”)
如图所示,质量为m的木块置于斜面上,木块与斜面间的动摩擦因数为μ,在外力作用下,斜面以加速度a沿水平方向向右做匀加速运动,运动中物体m与斜面体相对静止.则木块受到的重力不做功,受到的支持力做负功,受到的摩擦力做正功(填“正功”,“负功”或“不做功”)