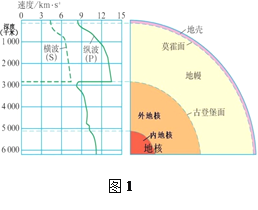
题目内容
【题目】如图所示,固定的长直水平轨道MN 与位于竖直平面内的光滑半圆轨道相接,圆轨道半径为R ,PN 恰好为该圆的一条竖直直径。可视为质点的物块A 和B 紧靠在一起静止于N 处,物块A 的质量 mA=2m,B的质量mB=m,两物块在足够大的内力作用下突然分离,分别沿轨道向左、右运动,物块B 恰好能通过P 点。已知物块A 与MN 轨道间的动摩擦因数为![]() ,重力加速度为g ,求:
,重力加速度为g ,求:

(1)物块B 运动到P 点时的速度大小vP;
(2)两物块刚分离时物块B 的速度大小vB;
(3)物块A 在水平面上运动的时间t 。
【答案】![]()
【解析】
试题分析:(1)物体B 在竖直平面内做圆周运动,在P 点时重力提供向心力
由![]()
(2)两物块分离后B 物体沿圆轨道向上运动,仅重力做负功
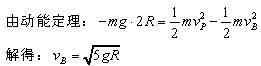
(3)物块A 与物块B 由足够大的内力突然分离,分离瞬间内力远大于外力,两物块在水平方向上动量守恒,
之后物体A 做匀减速直线运动,由牛顿第二定律得:![]()
由运动学公式![]()

练习册系列答案
相关题目