题目内容
2.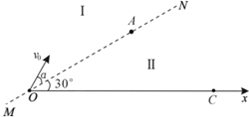 如图所示,在纸面内有一条过原点O的虚线MN,MN与x轴正方向的夹角为30°,在MN上有一点A,OA=L,在x轴上有一点C,坐标为xc=($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{15}}{6}$)L.空间有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,虚线MN是它们的理想边界,区域Ⅰ的磁感应强度的大小为B.在原点O处有一粒子源,可在纸面内向区域Ⅰ发射质量相同、电荷量相同、速率不同的正粒子,正粒子的速度方向与MN的夹角α在0~π的范围内.其中,一入射方向为α=30°、速度大小为v0的粒子射入区域Ⅰ,从A点第一次进入区域Ⅱ,从C点第一次穿过x轴.不计粒子的重力和粒子间的相互作用力.
如图所示,在纸面内有一条过原点O的虚线MN,MN与x轴正方向的夹角为30°,在MN上有一点A,OA=L,在x轴上有一点C,坐标为xc=($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{15}}{6}$)L.空间有两个方向都垂直纸面向外的匀强磁场区域Ⅰ和Ⅱ,虚线MN是它们的理想边界,区域Ⅰ的磁感应强度的大小为B.在原点O处有一粒子源,可在纸面内向区域Ⅰ发射质量相同、电荷量相同、速率不同的正粒子,正粒子的速度方向与MN的夹角α在0~π的范围内.其中,一入射方向为α=30°、速度大小为v0的粒子射入区域Ⅰ,从A点第一次进入区域Ⅱ,从C点第一次穿过x轴.不计粒子的重力和粒子间的相互作用力.(1)求区域Ⅱ中磁场的磁感应强度大小B2;
(2)速度方向与MN的夹角α=30°的所有粒子中,有些粒子能够通过A点,求这些粒子的速度大小;
(3)粒子源射出的所有粒子中,有些粒子不能穿过x轴,求这些粒子的速度方向与MN的夹角α应满足的条件.
分析 (1)作出粒子在两磁场中的运动轨迹,根据半径公式和几何关系求出区域Ⅱ中磁场的磁感应强度大小.
(2)通过几何关系求出运动的轨道半径,结合半径公式求出粒子的速度大小,注意需考虑粒子从磁场Ⅰ向Ⅱ运动穿过A点,还有从从磁场Ⅱ向Ⅰ运动穿过A点.
(3)抓住粒子不能穿过x轴,结合粒子在磁场区域Ⅱ的轨道半径,结合几何关系求出粒子的速度方向与MN的夹角α应满足的条件.
解答  解:(1)当α=30°时,设速度为v0的粒子在磁场Ⅰ和Ⅱ中做圆周运动的圆心分别为O1、O2,轨道半径分别为r10、r20,
解:(1)当α=30°时,设速度为v0的粒子在磁场Ⅰ和Ⅱ中做圆周运动的圆心分别为O1、O2,轨道半径分别为r10、r20,
由牛顿第二定律:${r_{10}}=\frac{{m{v_0}}}{{q{B_{\;}}}}$①,${r_{20}}=\frac{{m{v_0}}}{{q{B_2}}}$②
粒子从A点沿x轴正方向进入磁场Ⅱ,在直角△O1AD中:${r}_{10}=\frac{L}{2sin30°}=L$③
在直角△O2CE中:$r_{20}^2={({r_{20}}-\frac{L}{2})^2}+{({x_C}-\frac{{\sqrt{3}}}{2}L)^2}$④
由④解得:${r_{20}}=\frac{2}{3}L$
由①②③④解得:${B_2}=\frac{3}{2}B$,$\frac{m}{q}=\frac{BL}{v_0}$⑤
(2)当α=30°时,速率为v的粒子在磁场Ⅰ和Ⅱ中做圆周运动的半径分别为r1、r2,
由半径公式:${r_1}=\frac{mv}{qB}$,${r_2}=\frac{mv}{{q{B_2}}}$
解得:${r_2}=\frac{2}{3}{r_1}$⑥
ⅰ.若粒子从磁场Ⅰ向Ⅱ运动穿过A点,由几何关系:L=nr1-(n-1)r2⑦
联立解得:$v=\frac{{3{v_0}}}{n+2},(n=1,2…)$
ⅱ.若粒子从磁场Ⅱ向Ⅰ运动穿过A点,由几何关系:L=n(r1-r2)⑧
联立解得:$v=\frac{{3{v_0}}}{n},(n=1,2…)$
(3)设粒子在磁场Ⅰ和Ⅱ中做圆周运动的圆心分别为O3、O4,
由几何关系:OP=2r1sinα
PG=OPsin30°,∠O4PG=α-30°
PG≥r2+r2cos(α-30°)
联立解得:$sinα≥1+\frac{{\sqrt{3}}}{2}cosα$
故:α≥90°
答:(1)区域Ⅱ中磁场的磁感应强度大小为$\frac{3}{2}$B;
(2)这些粒子的速度大小为$\frac{3{v}_{0}}{n+2}$,(n=1,2…)或$\frac{3{v}_{0}}{n}$,(n=1,2…);
(3)这些粒子的速度方向与MN的夹角α应满足的条件为α≥90°.
点评 带电粒子通过磁场的边界时,如果边界是直线,根据圆的对称性得到,带电粒子入射速度方向与边界的夹角等于出射速度方向与边界的夹角,这在处理有界磁场的问题常常用到.本题难度较大,是试卷中的压轴题

 如图所示,A、B是某个点电荷电场中的一根电场线,在线上O点放一个自由的负电荷,它将沿电场线向B点运动,下列判断中哪些是正确的( )
如图所示,A、B是某个点电荷电场中的一根电场线,在线上O点放一个自由的负电荷,它将沿电场线向B点运动,下列判断中哪些是正确的( )| A. | 电场线由B指向A,φA<φB | |
| B. | 电场线由B指向A,φA>φB | |
| C. | 电场线由A指向B,EA>EB | |
| D. | 电场线由B指向A,该电荷作加速运动,其加速度越来越小 |
| A. | 电磁感应现象是牛顿发现 | |
| B. | 交流发电机产生的电流方向改变 | |
| C. | 升压变压器的原、副线圈匝数不相同 | |
| D. | 远距离输电要用高电压,是为了减少输电线上的电能损失 |
 如图是工厂自动化包装生产线的部分示意图,生产线将装有产品的包装盒通过水平传送带输送至自动装箱机装箱.由于可能有包装盒没装产品,为在装箱前将空盒拣出,有人采用了一种简单办法:在传送带旁加装鼓风机产生一个风力作用区,使包装盒受到垂直于传送带运动方向、大小恒定的水平风力,让原本和传送带一起匀速运动的空盒滑离传送带而装有产品的盒子仍和传送带一起匀速前进.下列对空盒在风力作用区中的运动分析正确的是( )
如图是工厂自动化包装生产线的部分示意图,生产线将装有产品的包装盒通过水平传送带输送至自动装箱机装箱.由于可能有包装盒没装产品,为在装箱前将空盒拣出,有人采用了一种简单办法:在传送带旁加装鼓风机产生一个风力作用区,使包装盒受到垂直于传送带运动方向、大小恒定的水平风力,让原本和传送带一起匀速运动的空盒滑离传送带而装有产品的盒子仍和传送带一起匀速前进.下列对空盒在风力作用区中的运动分析正确的是( )| A. | 空盒做直线运动,速度方向和风力方向相同 | |
| B. | 空盒做匀变速曲线运动 | |
| C. | 空盒在传送带运动方向的速度分量一直减小 | |
| D. | 空盒做直线运动,速度方向介于风力和传送带运动方向之间 |
 如图所示,两根完全相同的光滑的$\frac{1}{4}$圆弧轨道,半径为r,间距为L,它们的高度相同,即a、b在同一水平面上,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻不计的金属棒从轨道最低位置cd开始,在拉力作用下以初速度v0向右沿轨道做匀速圆周运动至ab处,已知cd棒切割磁感线产生的感应电动势按余弦规律变化.则该过程中( )
如图所示,两根完全相同的光滑的$\frac{1}{4}$圆弧轨道,半径为r,间距为L,它们的高度相同,即a、b在同一水平面上,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻不计的金属棒从轨道最低位置cd开始,在拉力作用下以初速度v0向右沿轨道做匀速圆周运动至ab处,已知cd棒切割磁感线产生的感应电动势按余弦规律变化.则该过程中( )| A. | 通过R的电流方向为由e到f | B. | 通过R的电流方向为由f到e | ||
| C. | 流过R的电量为$\frac{πBLr}{2R}$ | D. | R上产生的热量为$\frac{{π{B^2}{L^2}r{v_0}}}{4R}$ |
 经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由两颗相距较近的恒星组成,每颗恒星的半径远小于两颗恒星之间的距离,而且双星系统一般远离其他天体.如图,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上某-定点O点做匀速圆周运动,现测得两颗星球之间的距离为L,质量之比为m1:m2=3:2,则可知( )
经长期观测,人们在宇宙中已经发现了“双星系统”.“双星系统”由两颗相距较近的恒星组成,每颗恒星的半径远小于两颗恒星之间的距离,而且双星系统一般远离其他天体.如图,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上某-定点O点做匀速圆周运动,现测得两颗星球之间的距离为L,质量之比为m1:m2=3:2,则可知( )| A. | m1、m2做圆周运动的线速度之比为3:2 | |
| B. | m1、m2做圆周运动的角速度之比为1:1 | |
| C. | m1做圆周运动的半径为$\frac{3}{5}$l | |
| D. | m2做圆周运动的半径为$\frac{3}{5}$l |
| A. | “嫦娥三号”匀速飞行的速率为$\frac{2πNr}{t}$ | |
| B. | 月球的平均密度为$\frac{3πM{N}^{2}}{g{r}^{2}{t}^{2}}$ | |
| C. | “嫦娥三号”的质量为$\frac{4{π}^{2}{r}^{3}{N}^{2}}{g{R}^{2}{t}^{2}}$ | |
| D. | 月球受地球的引力为$\frac{4{π}^{2}M{r}^{3}{N}^{2}}{{L}^{2}{t}^{2}}$ |
 如图所示,质量为m=5.0kg的物体,在F=20N的水平拉力作用下沿水平面匀速运动,取g=10m/s2,求:
如图所示,质量为m=5.0kg的物体,在F=20N的水平拉力作用下沿水平面匀速运动,取g=10m/s2,求: