题目内容

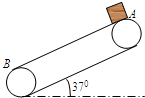精英家教网如图所示，传送带与水平方向夹37°角，在皮带轮带动下传送带以恒定速度
v=2m/s速度沿逆时针方向转动．可视为质点的小物块无初速地放在传送带A点，物块与传送带间的动摩擦因数为0.5，两皮带轮之间的距离L=3.2m．，已知sin37°=0.6，g取10m/s2，求
（1）小物块在传送带上运动时间；
（2）小物块在皮带上滑过后会留下痕迹的长度．
分析：传送带上对应于行李最初放置的一点通过的位移与行李做匀加速运动直至与传送带共同运动时间内通过的位移之差即是擦痕的长度
解答：解：（1）物体刚放到皮带上时做加速运动，则物块速度达到v0前的过程中，
由牛顿第二定律有：mgsinθ+μmgcosθ=ma1，
代入数据解得a1=10 m/s2
经历时间 t1=
V0
a1
=0.2s
物块位移 x1′=
V0t
2
=0.2m
皮带在此时间内运动的距离X1=V0t1=0.4m
划出痕迹的长度△L1=x1-x1'=0.2 m
物块的速度达到v0之后
由牛顿第二定律有：mgsinθ-μmgcosθ=ma2，
代入数据解得a2=2 m/s2
到脱离皮带这一过程，经历时间t2
x2′=L-x1′=v0 t2+
1
2
a2t
2
2
解得t2=1 s
此过程中皮带的位移x2=v0t2=2 m
△L2=x2'-x2=3 m-2 m=1 m
由于△L2＞△L1，所以痕迹长度为△L2=1 m．
△L=△L2-△L1=0.8m
在传送带上的时间为t=t1+t2=1.2s
答：（1）小物块在传送带上运动时间1.2s；
（2）小物块在皮带上滑过后会留下痕迹的长度0.8m．
点评：解决本题的关键会根据受力判断行李的运动情况，容易犯错的地方是行李的位移大小当作行李相对带留下的痕迹长度，实际上两者参考系不同，前者对地，后者对传送带
练习册系列答案
相关题目
如图所示为一皮带传送装置，皮带保持匀速率运动，货物由静止放到传送带上，被传送带向下传送，其运动的v-t图象如图乙所示．
解答下列问题（计算中取
2
=1.41，
3
=1.73）：
（l）皮带的速度：
（2）皮带与水半面间的夹角θ及货物与皮带之间的动摩擦因数μ的大小．
（3）如果货物是用麻袋装载的石灰粉，当一件货物被运送后，发现这件货物在皮带上留有一段l=4.0m长的白色痕迹，请由此推断该件货物的传送时间和传送距离．
“潮汐发电”是海洋能利用中发展最早、规模最大、技术较成熟的一种方式．某海港的货运码头，就是利用“潮汐发电”为皮带式传送机供电，图1所示为皮带式传送机往船上装煤．本题计算中取sin18°=0.31，cos18°=0.95，水的密度ρ=1.0×103kg/m3，g=10m/s2．
（1）皮带式传送机示意图如图2所示，传送带与水平方向的角度θ=18°，传送带的传送距离为L=51.8m，它始终以v=1.4m/s的速度运行．在传送带的最低点，漏斗中的煤自由落到传送带上（可认为煤的初速度为0），煤与传送带之间的动摩擦因数μ=0.4．求：从煤落在传送带上到运至传送带最高点经历的时间t；
（2）图3为潮汐发电的示意图．左侧是大海，中间有水坝，水坝下装有发电机，右侧是水库．当涨潮到海平面最高时开闸，水由通道进入海湾水库，发电机在水流的推动下发电，待库内水面升至最高点时关闭闸门；当落潮到海平面最低时，开闸放水发电．设某潮汐发电站发电有效库容V=3.6×106m3，平均潮差△h=4.8m，一天涨落潮两次，发电四次．水流发电的效率η1=10%．求该电站一天内利用潮汐发电的平均功率P；
（3）传送机正常运行时，1秒钟有m=50kg的煤从漏斗中落到传送带上．带动传送带的电动机将输入电能转化为机械能的效率η2=80%，电动机输出机械能的20%用来克服传送带各部件间的摩擦（不包括传送带与煤之间的摩擦）以维持传送带的正常运行．若用潮汐发电站发出的电给传送机供电，能同时使多少台这样的传送机正常运行？
精英家教网

“潮汐发电”是海洋能利用中发展最早、规模最大、技术较成熟的一种方式．某海港的货运码头，就是利用“潮汐发电”为皮带式传送机供电，如图所示为皮带式传送机往船上装煤．本题计算中取sin18o＝0.31，cos18o＝0.95，水的密度ρ＝1.0×103 kg/m3，g＝10 m/s2．

(1)皮带式传送机示意图如下图所示，传送带与水平方向的角度θ＝18o，传送带的传送距离为L＝51.8 m，它始终以v＝1.4 m/s的速度运行．在传送带的最低点，漏斗中的煤自由落到传送带上(可认为煤的初速度为0)，煤与传送带之间的动摩擦因数μ＝0.4．求：从煤落在传送带上到运至传送带最高点经历的时间t；

(2)下图为潮汐发电的示意图．左侧是大海，中间有水坝，水坝下装有发电机，右侧是水库．当涨潮到海平面最高时开闸，水由通道进入海湾水库，发电机在水流的推动下发电，待库内水面升至最高点时关闭闸门；当落潮到海平面最低时，开闸放水发电．设某潮汐发电站发电有效库容V＝3.6×106 m3，平均潮差Δh＝4.8 m，一天涨落潮两次，发电四次．水流发电的效率η1＝10％．求该电站一天内利用潮汐发电的平均功率P；

(3)传送机正常运行时，1秒钟有m＝50 kg的煤从漏斗中落到传送带上．带动传送带的电动机将输入电能转化为机械能的效率η2＝80%，电动机输出机械能的20%用来克服传送带各部件间的摩擦(不包括传送带与煤之间的摩擦)以维持传送带的正常运行．若用潮汐发电站发出的电给传送机供电，能同时使多少台这样的传送机正常运行？

为将货物传送到离地面一定高度的水平台C上，采用如图所示的传送带? 装置进行传送，传送带的皮带以一定的速度v顺时针转动且不打滑。将? 货物由静止放置在传送带底端A处，货物随皮带到达平台C。货物在皮? 带上发生相对滑动时，会留下痕迹。已知每件货物与皮带间的动摩擦因数均为，货物所受的最大静摩擦力等于滑动摩擦力，传送带斜面的长度为L。若皮带的倾角、运行速度秒和货物的质量m都可以调节(、L不变)，且始终满足tan <。则以下说法正确的是

A．当速度v一定时，倾角越大，传送时间越短

B．当倾角一定时，若传送带以另一速度运行，则传送时间不可能相同

C．当倾角和速度v一定时，货物的质量m越大，货物与皮带问因摩擦而产生的热量越多

D．当倾角和速度v一定时，货物的质量m越大，皮带上留下的痕迹越长

 

为将货物传送到离地面一定高度的水平台C上，采用如图所示的传送带装置进行传送，传送带的皮带以一定的速度v顺时针转动且不打滑。将 货物由静止放置在传送带底端A处，货物随皮带到达平台C。货物在皮 带上发生相对滑动时，会留下痕迹。已知每件货物与皮带间的动摩擦因数均为，货物所受的最大静摩擦力等于滑动摩擦力，传送带斜面的长度为L。若皮带的倾角、运行速度秒和货物的质量m都可以调节(、L不变)，且始终满足tan <。则以下说法正确的是

A．当速度v一定时，倾角越大，传送时间越短

B．当倾角一定时，若传送带以另一速度运行，则传送时间不可能相同

C．当倾角和速度v一定时，货物的质量m越大，货物与皮带问因摩擦而产生的热量越多

D．当倾角和速度v一定时，货物的质量m越大，皮带上留下的痕迹越长

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网