题目内容
如图所示，一电子沿Ox轴射入电场，在电场中的运动轨迹为OCD，已知. |
| OA |
. |
| AB |
分析：电子沿Ox轴射入匀强电场，做类平抛运动，水平方向做匀速直线运动，已知
=
，可知时间关系，竖直方向做匀加速运动，由运动学公式可分析速度关系，并能得到竖直位移的关系，由动能定理分析动能变化量的关系．
. |
| OA |
. |
| AB |
解答：解：A、B电子沿Ox轴射入匀强电场，做类平抛运动，水平方向做匀速直线运动，已知
=
，则电子从O到C与从C到D的时间相等．电子在竖直方向上做初速度为零的匀加速运动，则有vcy=atOC，vDy=atOD，所以 vcy：vDy=tOC：tOD=1：2．故A正确，B错误．
C、D根据匀变速直线运动的推论可知，在竖直方向上：yOC：yOD=1：4，根据动能定理得
△Ek1=qEyOC，△Ek2=qEyOD，则得，△Ek1：△Ek2=1：4．故C错误，D正确．
故选AD
. |
| OA |
. |
| AB |
C、D根据匀变速直线运动的推论可知，在竖直方向上：yOC：yOD=1：4，根据动能定理得
△Ek1=qEyOC，△Ek2=qEyOD，则得，△Ek1：△Ek2=1：4．故C错误，D正确．
故选AD
点评：本题是类平抛运动问题，运用运动的分解法研究，灵活运用比例法求解，比较简单．
练习册系列答案
相关题目
如图所示，一电子沿等量异种电荷的中垂线由A→O→B，匀速飞过，电子重力不计，则电子所受的另一外力的大小和方向变化情况（ ）
（2009?上海模拟）如图所示，一电子沿等量异种电荷的中垂线由A→O→B匀速飞过，电子重力不计，则电子除电场力外所受其他力的合力的大小和方向变化情况是（ ）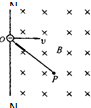
如图所示，一电子沿垂直挡板NN′方向以速度υ=8.0×106m/s从O孔射入匀强磁场中，磁场方向垂直纸面向里，磁感应强度为B=9.1×10-4T．运动中电子经某点P，OP=0.05m，求电子由O运动至P点的时间．（电子的质量m=9.1×10-31kg，电子的电量e=-1.6×10-19C，π≈3）
