题目内容
如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC竖直,下端A与光滑的水平轨道相切。一小球沿水平轨道进入竖直圆轨道,通过最高点C时对轨道的压力为其重力的3倍。不计空气阻力,g取10m/s2。求:
(1)小球在A点的速度大小;
(2)小球的落地点到A点的距离。
(1)小球在A点的速度大小;
(2)小球的落地点到A点的距离。

(1)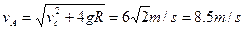 (2)
(2)
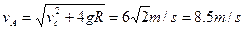 (2)
(2)
(1)设小球的质量为m,它通过最高点C时的速度为vc,根据牛顿第二定律,有
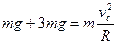 …………2分
…………2分
解得:vc="6m/s " ………………1分
设小球在A点的速度大小为vA,以地面为参考平面,根据机械能守恒定律,有:
 …………2分
…………2分
解得: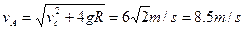 …………1分
…………1分
(2)小球离开C点后作平抛运动,根据 …………2分
…………2分
它在空中运动的时间为 t="0.6s" …………1分
小球的落地点到A点的距离为 …………1分
…………1分
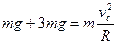 …………2分
…………2分解得:vc="6m/s " ………………1分
设小球在A点的速度大小为vA,以地面为参考平面,根据机械能守恒定律,有:
 …………2分
…………2分 解得:
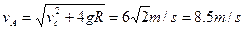 …………1分
…………1分(2)小球离开C点后作平抛运动,根据
 …………2分
…………2分它在空中运动的时间为 t="0.6s" …………1分
小球的落地点到A点的距离为
 …………1分
…………1分
练习册系列答案
相关题目
 、跳台、着陆坡、终止区组成。运动员脚着专用滑雪板,从起滑台起滑,在助滑道下滑加速后起跳,于台端飞出,沿抛物线在空中飞行一段时间后,落在着陆坡上继续滑行,最后停止在终止区。如图为一跳台滑雪场地,助滑坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=10m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差h1=35m,竖直跳台CD高度差为h2=5m,跳台底端与倾角为37°斜坡DE相连。运动员连同滑雪装备总质量为80kg,从A点由静止滑下,通过C点直接飞到空中,飞行一段时间落到着陆坡上,测得着陆坡上落点E到D点距离为125m(小计空气阻力,g取10m/s2。,sin37°=0.6,cos37°=0.8)。求:
、跳台、着陆坡、终止区组成。运动员脚着专用滑雪板,从起滑台起滑,在助滑道下滑加速后起跳,于台端飞出,沿抛物线在空中飞行一段时间后,落在着陆坡上继续滑行,最后停止在终止区。如图为一跳台滑雪场地,助滑坡由AB和BC组成,AB是倾角为37°的斜坡,BC是半径为R=10m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,如图所示,AB竖直高度差h1=35m,竖直跳台CD高度差为h2=5m,跳台底端与倾角为37°斜坡DE相连。运动员连同滑雪装备总质量为80kg,从A点由静止滑下,通过C点直接飞到空中,飞行一段时间落到着陆坡上,测得着陆坡上落点E到D点距离为125m(小计空气阻力,g取10m/s2。,sin37°=0.6,cos37°=0.8)。求: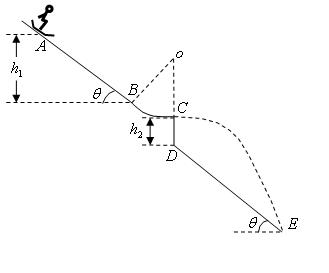
 的速度大小
的速度大小 毛巾长度比为1:3,见图a,AA'与地面的距离为h(h>l),毛巾质量为m,不计空气阻力,取重力加速度为g.
毛巾长度比为1:3,见图a,AA'与地面的距离为h(h>l),毛巾质量为m,不计空气阻力,取重力加速度为g.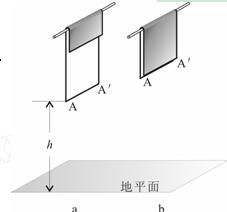
 圆弧形光滑轨道ABC,放置在竖直平面内,轨道半径为R,在A点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m的小球从A处正上方某处由静止释放,不考虑空气阻力,若小球能从C点射出并打到垫子上,小球距离A点的高度在什么范围.
圆弧形光滑轨道ABC,放置在竖直平面内,轨道半径为R,在A点与水平地面AD相接,地面与圆心O等高,MN是放在水平地面上长为3R、厚度不计的垫子,左端M正好位于A点.将一个质量为m的小球从A处正上方某处由静止释放,不考虑空气阻力,若小球能从C点射出并打到垫子上,小球距离A点的高度在什么范围.
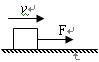
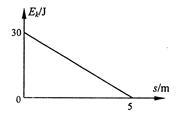
 ,则小物块从A运动到B的过程中,下列说法正确的是 ( )
,则小物块从A运动到B的过程中,下列说法正确的是 ( )