题目内容
 如图所示,在水平地面上有一质量为m的物体,在斜向上与水平方向成θ角的拉力F的作用下,物体由静止开始沿水平面做匀加速直线运动,在时间t内物体通过的位移为s,求:
如图所示,在水平地面上有一质量为m的物体,在斜向上与水平方向成θ角的拉力F的作用下,物体由静止开始沿水平面做匀加速直线运动,在时间t内物体通过的位移为s,求:(1)拉力F在时间t内所做的功;
(2)在t秒末拉力F做功的瞬时功率;
(3)物体与水平面之间的动摩擦因数为μ.
分析:(1)根据功的定义式求力F在时间t内做的功;
(2)根据P=Fvcosθ求力F的瞬时功率;
(3)根据位移时间关系求解出加速度a,再根据受力分析求出摩擦力f,由f=μN反推出动摩擦因数μ.
(2)根据P=Fvcosθ求力F的瞬时功率;
(3)根据位移时间关系求解出加速度a,再根据受力分析求出摩擦力f,由f=μN反推出动摩擦因数μ.
解答:解:(1)根据功的定义式可知
拉力F在时间t内所做的功为W=Fscosθ
(2)设在t秒末物体的速度为v,由于物体做初速度为0的匀加速直线运动,平均速度
=
=
则有s=
t ①
设在t秒末拉力F做功的瞬时功率为P,则有P=Fvcosθ ②
由①②两式得:P=
(3)设物体运动的加速度a,对物体进行受力分析如图所示
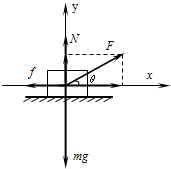 ,
,
根据题意有:
s=
at2 ③
f=μN ④
N+Fsinθ=mg ⑤
Fcosθ-f=ma ⑥
由③④⑤⑥可解得:μ=
答:(1)拉力F在t时间内做功W=Fscosθ
(2)在t秒末拉力做功的瞬时功率为P=
(3)物体与水平面间的动摩擦因数为μ=
拉力F在时间t内所做的功为W=Fscosθ
(2)设在t秒末物体的速度为v,由于物体做初速度为0的匀加速直线运动,平均速度
. |
| v |
| v0+v |
| 2 |
| v |
| 2 |
则有s=
| v |
| 2 |
设在t秒末拉力F做功的瞬时功率为P,则有P=Fvcosθ ②
由①②两式得:P=
| 2Fscosθ |
| t |
(3)设物体运动的加速度a,对物体进行受力分析如图所示
 ,
,根据题意有:
s=
| 1 |
| 2 |
f=μN ④
N+Fsinθ=mg ⑤
Fcosθ-f=ma ⑥
由③④⑤⑥可解得:μ=
| Ft2cosθ-2ms |
| (mg-Fsinθ)t2 |
答:(1)拉力F在t时间内做功W=Fscosθ
(2)在t秒末拉力做功的瞬时功率为P=
| 2Fscosθ |
| t |
(3)物体与水平面间的动摩擦因数为μ=
| Ft2cosθ-2ms |
| (mg-Fsinθ)t2 |
点评:掌握功的定义式、瞬时功率的表达式和正确的受力分析根据牛顿第二定律求解合外力与加速度是解决本题的关键.

练习册系列答案
相关题目
 (2010?宝山区一模)如图所示,在水平地面附近小球B以初速度v斜向上瞄准另一小球A射出,恰巧在B球射出的同时,A球由静止开始下落,不计空气阻力.则两球在空中运动的过程中( )
(2010?宝山区一模)如图所示,在水平地面附近小球B以初速度v斜向上瞄准另一小球A射出,恰巧在B球射出的同时,A球由静止开始下落,不计空气阻力.则两球在空中运动的过程中( ) 如图所示,在水平地面MN上方空间存在一垂直纸面向里、磁感应强度B=1T的有界匀强磁场区域,上边界EF距离地面的高度为H.正方形金属线框abcd的质量m=0.02kg、边长L=0.1m(L<H),总电阻R=0.2Ω,开始时线框在磁场上方,ab边距离EF高度为h,然后由静止开始自由下落,abcd始终在竖直平面内且ab保持水平.线框从开始运动到ab边刚要落地的过程中(g取10m/s2):
如图所示,在水平地面MN上方空间存在一垂直纸面向里、磁感应强度B=1T的有界匀强磁场区域,上边界EF距离地面的高度为H.正方形金属线框abcd的质量m=0.02kg、边长L=0.1m(L<H),总电阻R=0.2Ω,开始时线框在磁场上方,ab边距离EF高度为h,然后由静止开始自由下落,abcd始终在竖直平面内且ab保持水平.线框从开始运动到ab边刚要落地的过程中(g取10m/s2): 如图所示,在水平地面MN上方有一个粗糙绝缘平台PQ,高度为h=1m平台上方PR右侧有水平向右的有界匀强电场,PR左侧有竖直向上的匀强电场,场强大小均为E=1.1×l04N/C有一质量m=1.0×10-3kg、电荷量为q=-2.0×10-6C的滑块,放在距离平台左端P点L=1.2m处,滑块与平台间的动摩擦因数u=0.2,现给滑块水平向左的初速度v0=4m/s,取g=10m/s2,求:
如图所示,在水平地面MN上方有一个粗糙绝缘平台PQ,高度为h=1m平台上方PR右侧有水平向右的有界匀强电场,PR左侧有竖直向上的匀强电场,场强大小均为E=1.1×l04N/C有一质量m=1.0×10-3kg、电荷量为q=-2.0×10-6C的滑块,放在距离平台左端P点L=1.2m处,滑块与平台间的动摩擦因数u=0.2,现给滑块水平向左的初速度v0=4m/s,取g=10m/s2,求: (2009?日照一模)如图所示,在水平地面下埋着一条沿东西方向通有恒定电流的水平直导线.现用一串有灵敏电流计的闭合圆形检测线圈检测此通电直导线的位置.若不考虑地磁场的影响,检测线圈在水平面内,从距直导线很远处的北边移至距直导线很远处的南边的过程中,俯视检测线圈.下列说法正确的是( )
(2009?日照一模)如图所示,在水平地面下埋着一条沿东西方向通有恒定电流的水平直导线.现用一串有灵敏电流计的闭合圆形检测线圈检测此通电直导线的位置.若不考虑地磁场的影响,检测线圈在水平面内,从距直导线很远处的北边移至距直导线很远处的南边的过程中,俯视检测线圈.下列说法正确的是( ) 如图所示,在水平地面下有一条沿东西方向铺设的水平直导线,导线中通有自东向西稳定、强度较大的直流电流.现用一闭合的检测线圈(线圈中串有灵敏电流计,图中未画出)检测此通电直导线的位置,若不考虑地磁场的影响,在检测线圈位于水平面内,从距直导线很远处由北向南沿水平地面通过导线的上方并移至距直导线很远处的过程中,俯视检测线圈,其中的感应电流的方向是:( )
如图所示,在水平地面下有一条沿东西方向铺设的水平直导线,导线中通有自东向西稳定、强度较大的直流电流.现用一闭合的检测线圈(线圈中串有灵敏电流计,图中未画出)检测此通电直导线的位置,若不考虑地磁场的影响,在检测线圈位于水平面内,从距直导线很远处由北向南沿水平地面通过导线的上方并移至距直导线很远处的过程中,俯视检测线圈,其中的感应电流的方向是:( )