Question

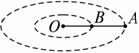
线段OB=AB，A、B两球质量相等，它们绕O点在光滑的水平面上以相同的角速度转动时，如图所示，两段线拉力之比T_AB：T_OB=

2：3

．

Answer 1

分析：两个小球以相同的角速度绕着O点做匀速圆周运动，分别对两个小球运用牛顿第二定律列式，即可求得两段绳子拉力之比T_AB：T_OB．

解答：解：设OB=AB=r，角速度为ω，每个小球的质量为m．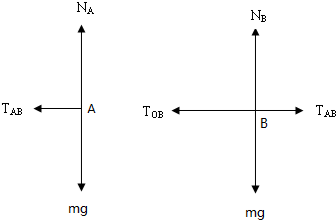
则根据牛顿第二定律得：
对A球：T_AB=mω²?2r
对B球：T_OB-T_AB=mω²?r
联立以上两式得：T_AB：T_OB=2：3
故答案为：2：3．

点评：本题要注意两球的加速度不同，只能用隔离进行研究，关键要分析它们向心力的来源．