题目内容
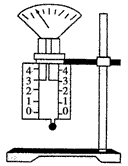
 如图所示是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为20cm,压强为p0=1×105Pa,现用竖直向下的外力压缩气体,使封闭的空气柱长度变为5cm.
如图所示是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为20cm,压强为p0=1×105Pa,现用竖直向下的外力压缩气体,使封闭的空气柱长度变为5cm.①若用足够长的时间缓慢压缩,求压缩后气体的压强;
②若快速压缩活塞,对气体做功 10J,同时气体向外散失的热量为2J,求该过程中气体内能的变化.
分析:(1)缓慢压缩气体过程,由于热交换,封闭气体的温度与环境温度相同,气体发生等温变化,根据玻意耳定律求解压缩后气体的压强;
(2)已知活塞对气体做功 10J和气体向外散失的热量为2J,根据热力学第一定律求解,该过程中气体内能的变化.
(2)已知活塞对气体做功 10J和气体向外散失的热量为2J,根据热力学第一定律求解,该过程中气体内能的变化.
解答:解:①设压缩后气体的压强为P,活塞的横截面积为S,10=20cm,1=5cm,V0=10S,V=lS,缓慢压缩,气体温度不变,
由玻意耳定律得:P0V0=PV
解出:p=4×105Pa
②活塞对气体做功W=10J,气体向外散失的热量2J,即Q=-2J,由热力学第一定律:△U=W+Q
代入解得△U=8J
答:①若用足够长的时间缓慢压缩,压缩后气体的压强是2×105Pa
②若压缩气体,对气体做功 10J,此过程气体向外散失的热量为2J,则气体的内能增加8J.
由玻意耳定律得:P0V0=PV
解出:p=4×105Pa
②活塞对气体做功W=10J,气体向外散失的热量2J,即Q=-2J,由热力学第一定律:△U=W+Q
代入解得△U=8J
答:①若用足够长的时间缓慢压缩,压缩后气体的压强是2×105Pa
②若压缩气体,对气体做功 10J,此过程气体向外散失的热量为2J,则气体的内能增加8J.
点评:对于气体状态变化问题,关键分析气体的状态参量,确定是何种变化过程,再列方程求解.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 (选修模块3-3)
(选修模块3-3)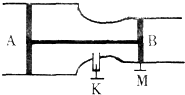 如图所示,一导热性能良好的容器水平放置,两端是直径不同的两个圆筒,里面各有一个活塞,其横截面积分别为
如图所示,一导热性能良好的容器水平放置,两端是直径不同的两个圆筒,里面各有一个活塞,其横截面积分别为 如图所示是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为3cm,此时气压表显示容器内压强人P1=1.0×105Pa.如果将活塞缓慢向下推动,直到封闭空气柱长度变为2cm时,气压表的示数是下列哪个( )
如图所示是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为3cm,此时气压表显示容器内压强人P1=1.0×105Pa.如果将活塞缓慢向下推动,直到封闭空气柱长度变为2cm时,气压表的示数是下列哪个( )