题目内容
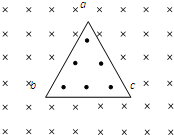如图所示，边长为L的等边三角形abc为两个匀强磁场的理想边界，三角形内的磁场方向垂直纸面向外，磁感应强度大小为B，三角形外的磁场范围足够大，方向垂直纸面向里，磁感应强度也为B．把一粒子源放在顶点a处，它将沿∠a的角平分线发射质量为m、电荷量为q、初速度为v0=| qBL |
| m |
分析：粒子在磁场中做匀速圆周运动，由牛顿第二定律可求得粒子在磁场中运动的半径；由粒子的运动情况可求得粒子回到a点的时间．
解答：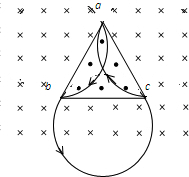
解：粒子所受到的洛仑兹力充当向心力，即Bqv0=m
，解得R=
=L，故A、B均错误；
粒子在磁场中的周期T=
，如图所示，粒子经历三段圆弧回到a点，则由几何关系可知，各段所对应的圆心角分别为：
，
，
，则带电粒子第一次返回到a点所用时间为
T=
，故C正确，D错误；
故选C．
解：粒子所受到的洛仑兹力充当向心力，即Bqv0=m| v02 |
| R |
| mv0 |
| Bq |
粒子在磁场中的周期T=
| 2πm |
| Bq |
| π |
| 3 |
| 5π |
| 3 |
| π |
| 3 |
| 7 |
| 6 |
| 7πm |
| 3qB |
故选C．
点评：本题的难点在于几何图象的确定应分析，要抓住三角形内外圆半径均为L，则可得出各自圆弧所对应的圆心角，从而确定粒子运动所经历的时间．
练习册系列答案
相关题目
如图所示，边长为L的正方形区域abcd内存在着匀强电场．电量为q、动能为Ek的带电粒子从a点沿ab方向进入电场，不计带电粒子的重力．
如图所示，边长为L的正方形线图abcd匝数为n、电阻为r，外电路的电阻为R，线圈位于磁感应强度为B的匀强磁场中，若线圈从图示位置开始，以角速度ω绕OO′轴匀速转动，则以下判断中正确的是（ ）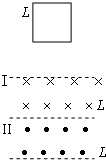
如图所示，边长为L的正方形导线框底边水平，且平行于正下方的磁场边界，正下方的匀强磁场宽度均为L，磁感强度等值反向，两磁场区域紧邻．当线框底边进入磁场I区域时，导线框恰好做匀速运动，这时导线框的电功率为P．则当导线框底边刚进入磁场II区域时，下列结论正确的是（ ）
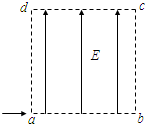如图所示，边长为L的正方形区域abcd内存在着匀强电场，一个质量为m、电量为q、初速度为v0的带电
如图所示，边长为L的正方形闭合线框，在磁感应强度为B的匀强磁场中，以一条边为轴，以角速度ω匀速转动，转轴与B垂直，线圈总电阻为R，导线电阻不计．下列说法中正确的是（ ）