题目内容
12. 如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,M=5m,A、B间动摩擦因素为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,M=5m,A、B间动摩擦因素为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:(1)A、B最后的速度大小和方向.
(2)A在B上相对运动的时间.
(3)平板车的最小长度.
分析 (1)A、B系统动量守恒,应用动量守恒定律可以求出速度.
(2)对B由动量定理可以求出运动时间.
(3)对系统,由能量守恒定律可以求出平板车的长度.
解答 解:(1)A、B系统动量守恒,以向右为正方向,
由动量守恒定律得:Mv0-mv0=(M+m)v,解得:v=$\frac{M-m}{M+m}$v0,
将M=5m代入上式可得:v=$\frac{2}{3}$v0,方向与平板车B初速度方向相同;
(2)对B车,由动量定理得:-μmgt=Mv-Mv0,解得:t=$\frac{5{v}_{0}}{3μg}$;
(3)由能量守恒定律的:μmgL=$\frac{1}{2}$(M+m)v02-$\frac{1}{2}$(M+m)v2,解得:L=$\frac{5{v}_{0}^{2}}{3μg}$;
答:(1)A、B最后的速度大小为:$\frac{2}{3}$v0,方向与平板车B初速度方向相同.
(2)A在B上相对运动的时间为$\frac{5{v}_{0}}{3μg}$.
(3)平板车的最小长度为$\frac{5{v}_{0}^{2}}{3μg}$.
点评 本题考查了动量守恒定律的应用,分析清楚物体运动过程是正确解题的关键,分析清楚运动过程后,应用动量守恒定律、动量定理与能量守恒定律可以解题,解题时要注意正方向的选择.

练习册系列答案
相关题目
3.质量为m的带电小球在竖直方向的匀强电场中以加速度a=$\frac{1}{3}$g从静止开始竖直向下运动了h的距离,则以下说法正确的是( )
| A. | 在整个过程中小球动能变化了mgh | |
| B. | 下落时电场力的瞬时功率为$\frac{1}{3}$mg$\sqrt{2gh}$ | |
| C. | 在整个过程中电势能增大了$\frac{2}{3}$mgh | |
| D. | 在整个过程中机械能减少了$\frac{1}{3}$mgh |
20. 构建和谐型、节约型社会深得民心,遍布于生活的方方面面.自动充电式电动车就是很好的一例,电动车的前轮装有发电机,发电机与蓄电池连接.当在骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机向蓄电池充电,将其他形式的能转化成电能储存起来.现有某人骑车以500J的初动能在粗糙的水平路面上滑行,第一次关闭自动充电装置,让车自由滑行,其动能随位移变化关系如图①所示;第二次启动自动充电装置,其动能随位移变化关系如图②所示,则第二次向蓄电池所充的电能是( )
构建和谐型、节约型社会深得民心,遍布于生活的方方面面.自动充电式电动车就是很好的一例,电动车的前轮装有发电机,发电机与蓄电池连接.当在骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机向蓄电池充电,将其他形式的能转化成电能储存起来.现有某人骑车以500J的初动能在粗糙的水平路面上滑行,第一次关闭自动充电装置,让车自由滑行,其动能随位移变化关系如图①所示;第二次启动自动充电装置,其动能随位移变化关系如图②所示,则第二次向蓄电池所充的电能是( )
 构建和谐型、节约型社会深得民心,遍布于生活的方方面面.自动充电式电动车就是很好的一例,电动车的前轮装有发电机,发电机与蓄电池连接.当在骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机向蓄电池充电,将其他形式的能转化成电能储存起来.现有某人骑车以500J的初动能在粗糙的水平路面上滑行,第一次关闭自动充电装置,让车自由滑行,其动能随位移变化关系如图①所示;第二次启动自动充电装置,其动能随位移变化关系如图②所示,则第二次向蓄电池所充的电能是( )
构建和谐型、节约型社会深得民心,遍布于生活的方方面面.自动充电式电动车就是很好的一例,电动车的前轮装有发电机,发电机与蓄电池连接.当在骑车者用力蹬车或电动自行车自动滑行时,自行车就可以连通发电机向蓄电池充电,将其他形式的能转化成电能储存起来.现有某人骑车以500J的初动能在粗糙的水平路面上滑行,第一次关闭自动充电装置,让车自由滑行,其动能随位移变化关系如图①所示;第二次启动自动充电装置,其动能随位移变化关系如图②所示,则第二次向蓄电池所充的电能是( )| A. | 200 J | B. | 250 J | C. | 300 J | D. | 500 J |
7.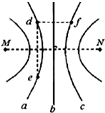 如图所示,真空中M、N 处放置两等量异号电荷,a、b、c表示电场中的3条等势线,d点和e点位于等势线a上,f 点位于等势线c上,df平行于MN.已知:一带负电的试探电荷从d点移动到f点时,试探电荷的电势能增加,则以下判断正确的是( )
如图所示,真空中M、N 处放置两等量异号电荷,a、b、c表示电场中的3条等势线,d点和e点位于等势线a上,f 点位于等势线c上,df平行于MN.已知:一带负电的试探电荷从d点移动到f点时,试探电荷的电势能增加,则以下判断正确的是( )
 如图所示,真空中M、N 处放置两等量异号电荷,a、b、c表示电场中的3条等势线,d点和e点位于等势线a上,f 点位于等势线c上,df平行于MN.已知:一带负电的试探电荷从d点移动到f点时,试探电荷的电势能增加,则以下判断正确的是( )
如图所示,真空中M、N 处放置两等量异号电荷,a、b、c表示电场中的3条等势线,d点和e点位于等势线a上,f 点位于等势线c上,df平行于MN.已知:一带负电的试探电荷从d点移动到f点时,试探电荷的电势能增加,则以下判断正确的是( )| A. | M点处放置的是负电荷 | |
| B. | d点的场强与f点的场强完全相同 | |
| C. | d点的电势高于f点的电势 | |
| D. | 若将带正电的试探电荷沿直线由d点移动到e点,则电场力先做正功、后做负功 |
17.质量为m的跳水运动员,从离地面高H的跳台上以速度v1斜向上跳起,跳起最大高度离跳台为h,最后以速度v2进入水中,空气阻力不能忽略,则下列说法正确的是( )
| A. | 运动员起跳时做的功为$\frac{1}{2}$mv${\;}_{1}^{2}$ | |
| B. | 从起跳到入水,重力对运动员做的功为mgH | |
| C. | 运动员克服空气阻力做的功为mg(H+h)-$\frac{1}{2}$mv${\;}_{2}^{2}$ | |
| D. | 运动员在下落过程中机械能总量保持不变 |
4.在同一高度,以不同速度同时水平抛出两个钢球,不计空气阻力,则两球( )
| A. | 同时落地 | B. | 水平位移相同 | C. | 加速度不同 | D. | 着地速度相同 |
 如图所示是某电场中的一簇等势面,甲等势面的电势为90V,乙等势面的电势为-10V,各相邻等势面间的电势差相等,将q=+1×10-8C的电荷从A点移到B点,电场力做功1×10-6J;在图中定性画出过A、B、C点三条电场线.
如图所示是某电场中的一簇等势面,甲等势面的电势为90V,乙等势面的电势为-10V,各相邻等势面间的电势差相等,将q=+1×10-8C的电荷从A点移到B点,电场力做功1×10-6J;在图中定性画出过A、B、C点三条电场线.