题目内容
5. 如图所示,在水平地面上有一个质量为5kg的物体,它受到与水平方向成53°角斜向上的25N的拉力时,恰好做匀速直线运动,g取10m/s2,问:当拉力为50N时,物体的加速度多大?物体由静止开始运动时,2s末物体的位移多大?(sin53°=0.8,cos53°=0.6)
如图所示,在水平地面上有一个质量为5kg的物体,它受到与水平方向成53°角斜向上的25N的拉力时,恰好做匀速直线运动,g取10m/s2,问:当拉力为50N时,物体的加速度多大?物体由静止开始运动时,2s末物体的位移多大?(sin53°=0.8,cos53°=0.6)
分析 对物体受力分析,抓住竖直方向和水平方向合力为零,根据共点力平衡求出动摩擦因数的大小;
根据牛顿第二定律,抓住竖直方向上的合力为零,结合水平方向上的合力求出物体的加速度.
根据运动学公式求出2s末物体的位移.
解答  解:由题意知,物体受力如图甲所示,由牛顿第二定律可得:
解:由题意知,物体受力如图甲所示,由牛顿第二定律可得:
F1cos 53°=Ff1①
FN+F1sin 53°=mg②
Ff1=μFN③
由①②③式得μ=$\frac{F1cos53°}{mg-F1sin53°}$=$\frac{25×0.6}{5×10-25×0.8}$=0.5
当拉力F2=50 N时,物体受力如图乙所示,由牛顿第二定律得:
F2cos 53°-Ff2=m…④
FN′+F2sin 53°-mg=0…⑤
Ff2=μFN′…⑥
由④⑤⑥式得物体的加速度为:
a=$\frac{50×0.6-0.5×(50-50×0.8)}{5}$=5 m/s2
根据运动学公式得2s内位移x=$\frac{1}{2}$at2=10 m.
答:当拉力为50N时,物体的加速度是5 m/s2,物体由静止开始运动时,2s末物体的位移是10 m.
点评 本题考考查牛顿第二定律的应用,属于已知受力求运动问题,解决本题的关键能够正确地受力分析,根据牛顿第二定律和共点力平衡进行求解.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
15.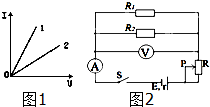 如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,闭合开关s后,当滑动变阻器触片P向下移动时,则( )
如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,闭合开关s后,当滑动变阻器触片P向下移动时,则( )
 如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,闭合开关s后,当滑动变阻器触片P向下移动时,则( )
如图1所示为两电阻R1和R2的伏安特性曲线.将电阻R1和R2接入如图2所示电路中,闭合开关s后,当滑动变阻器触片P向下移动时,则( )| A. | 电流表示数减小 | |
| B. | 电压表示数增大 | |
| C. | 电源的总功率增大 | |
| D. | 电阻R1上消耗的电功率大于电阻R2上消耗的电功率 |
16.如图是必修1课本中四幅插图,关于这四幅插图下列说法正确的是( )


| A. | 甲图中学生从如图姿势起立到直立站于体重计的过程中,体重计的示数先减少后增加 | |
| B. | 乙图中冰壶在冰面上的运动也可做曲线运动 | |
| C. | 丙图中赛车的质量不很大,却安装着强大的发动机,目的是为了获得很大的牵引力 | |
| D. | 丁图中高大的桥要造很长的引桥,从而减小桥面的坡度,来增大车辆重力沿桥面方向的分力,保证行车方便与安全 |
20.某同学用如图1所示的装置研究匀变速直线运动的规律.

(1)实验开始前不需要(填“需要”或“不需要”)平衡摩擦力,实验中不需要(填“需要”或“不需要”)保证悬挂的钩码质量要远小于小车的质量.
(2)实验中,从打出的多条纸带选取一条合适的纸带,并在其上取了O,A,B,C,D,E,F共7个计数点,(如图2每相邻两个计数点间还有四个计时点未画出)用刻度尺测出 A,B,C,D,E,F六个计数点到O点的距离并填在表格中
打点计时器所用交流电的频率为50Hz,则打点C时小车的速度为0.16m/s,小车运动的加速度为0.40ms2,从释放小车到打点C时,小车运动的时间为0.40s(结果都保留两位有效数字).

(1)实验开始前不需要(填“需要”或“不需要”)平衡摩擦力,实验中不需要(填“需要”或“不需要”)保证悬挂的钩码质量要远小于小车的质量.
(2)实验中,从打出的多条纸带选取一条合适的纸带,并在其上取了O,A,B,C,D,E,F共7个计数点,(如图2每相邻两个计数点间还有四个计时点未画出)用刻度尺测出 A,B,C,D,E,F六个计数点到O点的距离并填在表格中
| 线段 | OA | OB | OC | OD | OE | OF |
| 数据/cm | 0.54 | 1.53 | 2.92 | 4.76 | 7.00 | 9.40 |
17. 如图所示,在虚线包围的区域里存在着强度为E的匀强电场和磁感应强度为B的匀强磁场.已知从左方射来的一束电子穿过该区域时没有发生偏转,不计电子重力,这个区域中E和B的方向可能是( )
如图所示,在虚线包围的区域里存在着强度为E的匀强电场和磁感应强度为B的匀强磁场.已知从左方射来的一束电子穿过该区域时没有发生偏转,不计电子重力,这个区域中E和B的方向可能是( )
 如图所示,在虚线包围的区域里存在着强度为E的匀强电场和磁感应强度为B的匀强磁场.已知从左方射来的一束电子穿过该区域时没有发生偏转,不计电子重力,这个区域中E和B的方向可能是( )
如图所示,在虚线包围的区域里存在着强度为E的匀强电场和磁感应强度为B的匀强磁场.已知从左方射来的一束电子穿过该区域时没有发生偏转,不计电子重力,这个区域中E和B的方向可能是( )| A. | E和B都沿水平方向,并与电子运动方向相同 | |
| B. | E和B都沿水平方向,并与电子运动方向相反 | |
| C. | E竖直向上,B垂直纸面向外 | |
| D. | E竖直向上,B垂直纸面向里 |
14.两个大小分别为5N、3N的共点力,它们同向时的合力大小是( )
| A. | 2N | B. | 4N | C. | 8N | D. | 15N |
15.在研究下述运动时,能把物体看作质点的是( )
| A. | 研究地球的自转 | B. | 研究乒乓球的旋转 | ||
| C. | 研究火车从北京运行到上海 | D. | 研究转动的汽车轮胎 |

