题目内容
【题目】如图所示,将一小球以速度v0=3m/s的速度从A点水平抛出的同时,在倾角为37°的斜面顶端B点的滑块以VB=2.1m/s的初速度向下做匀加速直线运动,经过一段时间后小球恰好能够以垂直斜面的方向击中滑块,已知A、B两点间高度差![]() =0.2m,(小球和滑块均视为质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8),
=0.2m,(小球和滑块均视为质点,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8),
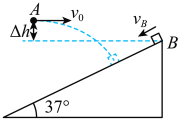
求:(1)小球从抛出到击中滑块所用的时间;
(2)小球下落的高度;
(3)滑块与斜面间的动摩擦因数
【答案】(1)0.4s (2)0.8m (3)0.5
【解析】
(1)根据平行四边形定则求出小球击中滑块时的竖直分速度,结合速度时间公式求出小球从抛出到击中滑块的时间.
(2)根据位移时间公式求出小球下落的高度.
(3)根据几何关系求出滑块下滑的位移,抓住时间相等,结合位移时间公式求出滑块的加速度,根据牛顿第二定律求出动摩擦因数的大小.
(1)根据平行四边形定则知,tan37°=![]() ,
,
解得小球击中滑块时的竖直分速度![]() ,
,
则小球从抛出到击中滑块所用的时间![]() .
.
(2)小球下落的高度h=![]() gt2=
gt2=![]() ×10×0.16m=0.8m.
×10×0.16m=0.8m.
(3)物块下滑的位移![]() ,
,
根据位移时间公式有:x=vBt+![]() at2,代入数据解得a=2m/s2,
at2,代入数据解得a=2m/s2,
根据牛顿第二定律得,a=![]() =gsinθ-μgcosθ,
=gsinθ-μgcosθ,
代入数据解得μ=0.5.

练习册系列答案
相关题目