题目内容
(1)光线以某一入射角从空气射入折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于
的某液体射入空气中正好发生全反射,入射角α等于
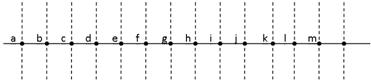
(2)如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置.一列横波以1m/s的速度水平向右传播,在t=0时刻到达质点a,且a开始由平衡位置向上振动,在t=1s时刻,质点a第一次达到最高点,求:
①这列波的波长和周期;
②从a开始振动,经过多长时间d点第一次向下达到最大位移;
③在上图中画出d点第一次向下达到最大位移时的波形图象.

| 3 |
30°
30°
;若光线以入射角α从折射率为| 2 |
45°
45°
.(2)如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置.一列横波以1m/s的速度水平向右传播,在t=0时刻到达质点a,且a开始由平衡位置向上振动,在t=1s时刻,质点a第一次达到最高点,求:
①这列波的波长和周期;
②从a开始振动,经过多长时间d点第一次向下达到最大位移;
③在上图中画出d点第一次向下达到最大位移时的波形图象.

分析:(1)根据几何知识确定入射角和折射角的关系,由折射定律求出折射角.由临界角公式sinC=
求出临界角.恰好发生全反射时,入射角恰好等于临界角.
(2)①a开始由平衡位置向上振动,经过
周期时间第一次到达波峰,求出周期,由波速公式求出波长.②分别求出波从a点传到d点的时间和d从平衡位置第一次向下达到最大位移的时间,两者之和即为所解.③d点第一次向下达到最大位移时,根据时间求出波传播的距离,再画出波形.
| 1 |
| n |
(2)①a开始由平衡位置向上振动,经过
| 1 |
| 4 |
解答:解:(1)设折射角为r,入射角为i,反射角为i′,由题,i′+r=90°,根据反射定律则有,i=i′,则i+r=90°
根据折射定律得
n=
=
=
=
,解得,r=30°
由临界角公式sinC=
=
,得C=45°
光线从液体射入空气中正好发生全反射,入射角恰好临界角,所以α=45°.
(2)①由题得
T=t=1s,则周期T=4s,由波速公式v=
得,λ=vT=4m
②从a开始振动,波传到d的时间为t1=3s,波传到d时,d点向上振动,再t2=
T=3s第一次到达波谷,则t=t1+t2=6s
③波在t=6s时间传播的距离为x=vt=6m,则波传到d点,画出波形如图.
故答案为:
(1)30°,45°
(2)①波长λ=4m,周期T=4s
②经t=6s后d点第一次向下达到最大位移.
③点d第一次向下达到最大位移时的波形图象如下图所示.

根据折射定律得
n=
| sini |
| sinr |
| sin(90°-r) |
| sinr |
| cosr |
| sinr |
| 3 |
由临界角公式sinC=
| 1 |
| n |
| ||
| 2 |
光线从液体射入空气中正好发生全反射,入射角恰好临界角,所以α=45°.
(2)①由题得
| 1 |
| 4 |
| λ |
| T |
②从a开始振动,波传到d的时间为t1=3s,波传到d时,d点向上振动,再t2=
| 3 |
| 4 |
③波在t=6s时间传播的距离为x=vt=6m,则波传到d点,画出波形如图.
故答案为:
(1)30°,45°
(2)①波长λ=4m,周期T=4s
②经t=6s后d点第一次向下达到最大位移.
③点d第一次向下达到最大位移时的波形图象如下图所示.

点评:几何光学根据几何知识求解入射角或折射角是常见思路.第2题分析质点的振动与波动的关系是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.
 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.
 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为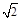 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.
 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.