题目内容
现要验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一物理规律.给定的器材如下:
一倾角可以调节的长斜面(如图1所示)小车、计时器一个、米尺.
(1)填入适当的公式或文字,完善以下实验步骤(不考虑摩擦力的影响):
①让小车自斜面上方一固定点A1从静止开始下滑至斜面底端A2,记下所用的时间t;
②用米尺测量A1与A2之间的距离x,则小车的加速度a=______;
③用米尺测量A1相对于A2的高度h.设小车所受重力为mg,则小车所受合外力F=______;
④改变______,重复上述测量;
⑤以h为横坐标,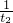 为纵坐标,根据实验数据作图.如能得到一条过原点的直线,则可以验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一规律.
为纵坐标,根据实验数据作图.如能得到一条过原点的直线,则可以验证“当质量一定时,物体运动的加速度与它所受的合外力成正比”这一规律.
(2)在“验证牛顿运动定律”的实验中,实验装置如图2中的甲所示,有一位同学通过实验测量作出了图乙中的A图线.试分析:
①A图线不通过坐标原点的原因是______;
②A图线上部弯曲的原因是______.

解:(1)小车做的是初速度为零的匀加速直线运动,根据运动规律:s= at2,解得:a=
at2,解得:a=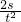 ;
;
(2)小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,sinθ=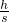 ,所以合力为:F=mgsinθ=
,所以合力为:F=mgsinθ=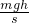 ;
;
(3)用动能定理可解得:h=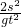 ,所以h与
,所以h与 成正比,我们需要改变h,所以需要:改变斜面的倾角或斜面高h
成正比,我们需要改变h,所以需要:改变斜面的倾角或斜面高h
(3)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
(4)①由图象可知,当小车所受拉力不为零时,加速度仍然没有产生,因此该实验的操作不当为:没有平衡摩擦力或平衡摩擦力不够.
②设小车与砝码的质量为M,小桶与砂子的质量为m,根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=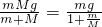
当m<<M时,绳子的拉力近似等于砂和砂桶的总重力.当小桶与砂子的质量为m变大后不能满足m<<M的条件,故图象弯曲,故应填:未满足钩码质量远小于小车质量.
故答案为: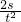 ;
;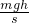 ;改变斜面的倾角或斜面高h;没有平衡摩擦力或平衡摩擦力不够;未满足钩码质量远小于小车质量.
;改变斜面的倾角或斜面高h;没有平衡摩擦力或平衡摩擦力不够;未满足钩码质量远小于小车质量.
分析:(1)小车做的是初速度为零的匀加速直线运动,根据运动规律:s= at2可求出加速度a.
at2可求出加速度a.
(2)小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,求出sinθ,即可求出合外力F.
(3)用动能定理可解得:h=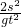 ,所以h与
,所以h与 成正比,所以我们需要改变h.
成正比,所以我们需要改变h.
(4)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
点评:(1)第一题的关键是找出实验原理,是重力沿斜面的分力做为合外力,最终得到h=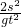 ,所以h与
,所以h与 成正比,来对实验数据进行分析.
成正比,来对实验数据进行分析.
(2)解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.其中平衡摩擦力的原因以及做法在实验中应当清楚.
 at2,解得:a=
at2,解得:a=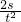 ;
;(2)小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,sinθ=
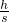 ,所以合力为:F=mgsinθ=
,所以合力为:F=mgsinθ=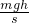 ;
;(3)用动能定理可解得:h=
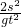 ,所以h与
,所以h与 成正比,我们需要改变h,所以需要:改变斜面的倾角或斜面高h
成正比,我们需要改变h,所以需要:改变斜面的倾角或斜面高h(3)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
(4)①由图象可知,当小车所受拉力不为零时,加速度仍然没有产生,因此该实验的操作不当为:没有平衡摩擦力或平衡摩擦力不够.
②设小车与砝码的质量为M,小桶与砂子的质量为m,根据牛顿第二定律得:
对m:mg-F拉=ma
对M:F拉=Ma
解得:F拉=
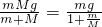
当m<<M时,绳子的拉力近似等于砂和砂桶的总重力.当小桶与砂子的质量为m变大后不能满足m<<M的条件,故图象弯曲,故应填:未满足钩码质量远小于小车质量.
故答案为:
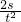 ;
;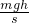 ;改变斜面的倾角或斜面高h;没有平衡摩擦力或平衡摩擦力不够;未满足钩码质量远小于小车质量.
;改变斜面的倾角或斜面高h;没有平衡摩擦力或平衡摩擦力不够;未满足钩码质量远小于小车质量.分析:(1)小车做的是初速度为零的匀加速直线运动,根据运动规律:s=
 at2可求出加速度a.
at2可求出加速度a.(2)小车所受的合外力是重力沿斜面的分力,大小为:mgsinθ,θ为斜面的夹角,求出sinθ,即可求出合外力F.
(3)用动能定理可解得:h=
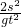 ,所以h与
,所以h与 成正比,所以我们需要改变h.
成正比,所以我们需要改变h.(4)根据牛顿第二定律和图象的特点可分析实验实验误差产生的原因.
点评:(1)第一题的关键是找出实验原理,是重力沿斜面的分力做为合外力,最终得到h=
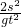 ,所以h与
,所以h与 成正比,来对实验数据进行分析.
成正比,来对实验数据进行分析.(2)解决实验问题首先要掌握该实验原理,了解实验的操作步骤和数据处理以及注意事项.其中平衡摩擦力的原因以及做法在实验中应当清楚.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 分享到
分享到- QQ空间
- 新浪微博
- 百度搜藏
- 人人网
- 腾讯微博
- 开心网
- 腾讯朋友
- 百度空间
- 豆瓣网
- 搜狐微博
- MSN
- QQ收藏
- 我的淘宝
- 百度贴吧
- 搜狐白社会
- 更多...
百度分享
一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:电磁打点计时器、米尺、纸带、复写纸片。
实验步骤:
(1)如图1所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后,固定在待测圆盘的侧面上,使得圆盘转动时,纸带可以卷在圆盘侧面上。
(2)启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
(3)经过一段时间,停止转动和打点,取下纸带,进行测量。
① 由已知量和测得量表示的角速度的表达式为ω= 。式中各量的意义是:
.
② 某次实验测得圆盘半径r=5.50×10-2m,得到纸带的一段如图2所示,求得角速度为 。
(1) (2)6.8/s。 |