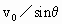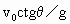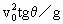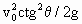题目内容
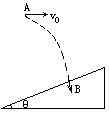
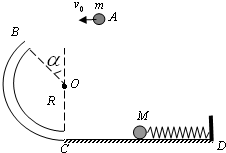 如图所示,在空中A点将质量为m=0.1kg的小球以某一水平速度抛出,将无碰撞地由B点进入竖直平面内半径R=
如图所示,在空中A点将质量为m=0.1kg的小球以某一水平速度抛出,将无碰撞地由B点进入竖直平面内半径R=| 13 | 12 |
(1)小球在A点抛出的水平初速度v0.
(2)小球运动到最低点C时,小球对轨道的压力FN的大小(结果保留一位有效数字)
(3)弹簧压缩过程中,弹簧具有的最大弹性势能Ep
(4)若只将弹簧右侧栓接的挡板改为栓接一个质量为M′=0.4kg的光滑小球,水平轨道足够长,其它条件保持不变,则三个小球在整个运动和相互作用过程中小球M′第二次达到最大速度时,小球M的速度是多少?
分析:1、小球在A点抛出做平抛运动,根据平抛运动规律求解;
2、小球由B点运动到C点的过程中,根据机械能守恒求出在C点速度,根据牛顿第二定律和牛顿第三定律求解;
3、两球相碰根据动量守恒,两球一起压弹簧到最短的过程中,当两球速度为零时,弹性势能最大,根据能量守恒求解;
4、根据动量守恒守恒和机械能守恒列出等式求解.
2、小球由B点运动到C点的过程中,根据机械能守恒求出在C点速度,根据牛顿第二定律和牛顿第三定律求解;
3、两球相碰根据动量守恒,两球一起压弹簧到最短的过程中,当两球速度为零时,弹性势能最大,根据能量守恒求解;
4、根据动量守恒守恒和机械能守恒列出等式求解.
解答:解:(1)设小球运动到B点时的竖直速度为vy,根据运动学规律得:
=2gh ①
在B点时,根据速度关系得
tanα=
②
综合①、②并代入已知得
v0=4m/s ③
(2)小球在B点时的速度
vB=
④
小球由B点运动到C点的过程中,根据机械能守恒有
m
=
m
+mgR(1+cosα) ⑤
在C点,根据牛顿第二定律有
FN-mg=m
⑥
由④、⑤、⑥式,并代入已知得FN=7N ⑦
根据牛顿第三定律得小球对轨道的压力为7N
(3)两球相碰根据动量守恒,规定初速度方向为正方向,
mvC=(m+M)v ⑧
两球一起压弹簧到最短的过程中,当两球速度为零时,弹性势能最大,
根据能量守恒得
(m+M)v2=Ep ⑨
由⑧、⑨式,并代入已知得Ep=0.8J
(4)三个小球在整个运动和相互作用过程中小球M′第二次达到最大速度时,该状态时弹簧处于原长,规定初速度方向为正方向,
根据动量守恒守恒列式:
(m+M)v=(m+M)v1+M′v2
根据机械能守恒列出等式:
(m+M)v2=
(m+M)
+
M′
列式解方程组得,v2=v,v1=0
所以当小球M′第二次达到最大速度时,小球M的速度是0.
答:(1)小球在A点抛出的水平初速度是4m/s.
(2)小球运动到最低点C时,小球对轨道的压力FN的大小是7N.
(3)弹簧压缩过程中,弹簧具有的最大弹性势能是0.8J
(4)三个小球在整个运动和相互作用过程中小球M′第二次达到最大速度时,小球M的速度是0.
| v | 2 y |
在B点时,根据速度关系得
tanα=
| vy |
| v0 |
综合①、②并代入已知得
v0=4m/s ③
(2)小球在B点时的速度
vB=
|
小球由B点运动到C点的过程中,根据机械能守恒有
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
在C点,根据牛顿第二定律有
FN-mg=m
| ||
| R |
由④、⑤、⑥式,并代入已知得FN=7N ⑦
根据牛顿第三定律得小球对轨道的压力为7N
(3)两球相碰根据动量守恒,规定初速度方向为正方向,
mvC=(m+M)v ⑧
两球一起压弹簧到最短的过程中,当两球速度为零时,弹性势能最大,
根据能量守恒得
| 1 |
| 2 |
由⑧、⑨式,并代入已知得Ep=0.8J
(4)三个小球在整个运动和相互作用过程中小球M′第二次达到最大速度时,该状态时弹簧处于原长,规定初速度方向为正方向,
根据动量守恒守恒列式:
(m+M)v=(m+M)v1+M′v2
根据机械能守恒列出等式:
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 2 |
列式解方程组得,v2=v,v1=0
所以当小球M′第二次达到最大速度时,小球M的速度是0.
答:(1)小球在A点抛出的水平初速度是4m/s.
(2)小球运动到最低点C时,小球对轨道的压力FN的大小是7N.
(3)弹簧压缩过程中,弹簧具有的最大弹性势能是0.8J
(4)三个小球在整个运动和相互作用过程中小球M′第二次达到最大速度时,小球M的速度是0.
点评:该题为平抛运动与圆周运动的结合的综合题,知道平抛运动的规律和牛顿第二定律求解得思路.
解决该题关键是掌握碰撞过程两球系统机械能守恒,动量也守恒,列出等式求解.
解决该题关键是掌握碰撞过程两球系统机械能守恒,动量也守恒,列出等式求解.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
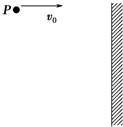 如图所示,在空中某一位置P将一个小球以初速度v0水平向右抛出,它和竖直墙壁碰撞时速度方向与水平方向成45°角,若将小球仍从P点以2v0的初速度水平向右抛出,下列说法中正确的是( )
如图所示,在空中某一位置P将一个小球以初速度v0水平向右抛出,它和竖直墙壁碰撞时速度方向与水平方向成45°角,若将小球仍从P点以2v0的初速度水平向右抛出,下列说法中正确的是( )| A、小球在两次运动过程中速度增量方向相同,大小之比为2:1 | ||
| B、小球第二次碰到墙壁前瞬时速度方向与水平方向成30°角 | ||
| C、小球第二次碰到墙壁时的动能为第一次碰到墙壁时动能的2倍 | ||
D、小球第二次碰到墙壁时的动能为第一次碰到墙壁时动能的
|
 (2008?临沂一模)如图所示,真空中O点处固定一点电荷Q,同时在O点通过绝缘细线悬挂一带电荷量为q质量为m的小球,开始时细线与小球处在水平位置且静止,释放后小球摆到最低点时,细线的拉力为4mg,则固定电荷Q在最低点B处产生的场强大小为( )
(2008?临沂一模)如图所示,真空中O点处固定一点电荷Q,同时在O点通过绝缘细线悬挂一带电荷量为q质量为m的小球,开始时细线与小球处在水平位置且静止,释放后小球摆到最低点时,细线的拉力为4mg,则固定电荷Q在最低点B处产生的场强大小为( ) 水平抛出一小球,飞行一段时间后,垂直地撞在倾角为
水平抛出一小球,飞行一段时间后,垂直地撞在倾角为 的斜面上的B点,由此求得
的斜面上的B点,由此求得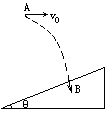
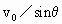
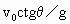
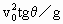
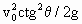
 水平抛出一小球,飞行一段时间后,垂直地撞在倾角为
水平抛出一小球,飞行一段时间后,垂直地撞在倾角为 的斜面上的B点,由此求得
的斜面上的B点,由此求得