题目内容
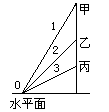
有三个光滑斜轨道1、2、3，它们的倾角依次是60°、45°和30°，这些轨道交于O点.现有位于同一竖直线上的三个小物体甲、乙、丙，分别沿这三个轨道同时从静止自由下滑，如图3-3-27所示.物体滑到O点的先后顺序是（ ）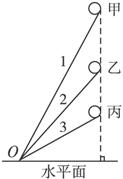
图3-3-27
A.甲最先，乙稍后，丙最后 B.乙最先，然后甲和丙同时到达
C.甲、乙、丙同时到达 D.乙最先，甲稍后，丙最后
思路解析：设直角三角形的底边长为d，当物体沿着与水平方向成θ角的斜面下滑时，加速度a=gsinθ，斜面长s=d/cosθ.所以物体沿斜面滑动的时间：
t=
=
=
，可见t的大小与θ有关，当θ角等于45°时，2θ等于90°，sin2θ=1，此时t值最小，因此乙球最先到达O点，选项A和选项D均错误.60°角和120°角的正弦值相等，因此甲球和乙球滑行的时间相同，同时到达O点，故选项B正确.
答案：B
练习册系列答案
相关题目
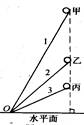
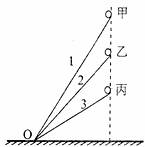
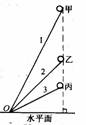
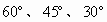，这些轨道交于O点，现有位于同一竖直线上的3个小物体甲、乙、丙，分别沿这3个轨道同时从静止自由下滑，如图所示，物体滑到O点的先后顺序是
