题目内容
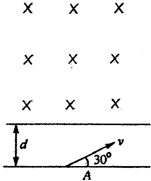 (2010?天津模拟)如图所示宽度为d的区域上方存在垂直纸面、方向向内、磁感应强度大小为B的无限大匀强磁场,现有一质量为m,带电量为+q的粒子在纸面内以某一速度从此区域下边缘上的A点射入,其方向与下边缘线成30°角,粒子能回到A点,(不计重力)试求:
(2010?天津模拟)如图所示宽度为d的区域上方存在垂直纸面、方向向内、磁感应强度大小为B的无限大匀强磁场,现有一质量为m,带电量为+q的粒子在纸面内以某一速度从此区域下边缘上的A点射入,其方向与下边缘线成30°角,粒子能回到A点,(不计重力)试求:(1)速度v的大小.
(2)粒子从A点出发,再次回到A点时所用的时间.
分析:(1)带电粒子进入匀强磁场时在洛伦兹力作用下做匀速圆周运动,射出磁场后做匀速直线运动,画出轨迹,由几何知识求出圆周运动轨迹半径,由牛顿第二定律求出速度v;
(2)已知带电粒子的质量与电量,则由周期公式可求出周期,并由入射的角度去确定运动的时间与周期的关系.由t=
求匀速直线运动的时间.
(2)已知带电粒子的质量与电量,则由周期公式可求出周期,并由入射的角度去确定运动的时间与周期的关系.由t=
| s |
| v |
解答: 解:(1)粒子运动轨迹如图所示,设粒子在磁场中的轨道半径为r,由图示的几何关系可知
解:(1)粒子运动轨迹如图所示,设粒子在磁场中的轨道半径为r,由图示的几何关系可知
r=
=2
d
则有 qvB=
解得 v=
此时粒子可按图中轨道返到A点.
(2)进入磁场前粒子匀速直线运动的距离
d1=
匀速直线运动的时间 t1=
进入磁场后就粒子做匀速圆周运动的时间 t2=
T
T=
从磁场出来到A点的时间 t3=t1
总时间 t=t1+t2+t3=
+
答:
(1)速度v的大小为
.
(2)粒子从A点出发,再次回到A点时所用的时间为
+
.
 解:(1)粒子运动轨迹如图所示,设粒子在磁场中的轨道半径为r,由图示的几何关系可知
解:(1)粒子运动轨迹如图所示,设粒子在磁场中的轨道半径为r,由图示的几何关系可知r=
| 2d |
| tan30° |
| 3 |
则有 qvB=
| mv2 |
| r |
解得 v=
2
| ||
| m |
此时粒子可按图中轨道返到A点.
(2)进入磁场前粒子匀速直线运动的距离
d1=
| d |
| sin30° |
匀速直线运动的时间 t1=
| d1 |
| v |
进入磁场后就粒子做匀速圆周运动的时间 t2=
| ||
| 2π |
T=
| 2πm |
| qB |
从磁场出来到A点的时间 t3=t1
总时间 t=t1+t2+t3=
2
| ||
| 3qB |
| 5πm |
| 3qB |
答:
(1)速度v的大小为
2
| ||
| m |
(2)粒子从A点出发,再次回到A点时所用的时间为
2
| ||
| 3qB |
| 5πm |
| 3qB |
点评:带电粒子在磁场中运动的题目关键要画出轨迹,一般按定圆心、画轨迹、求半径进行分析求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010?天津模拟)[选做题]氢原子发出a、b两种频率的光经三棱镜折射后的光路如图所示,若a光是由能级n=4向n=l跃迁时发出时,则b光可能是( )
(2010?天津模拟)[选做题]氢原子发出a、b两种频率的光经三棱镜折射后的光路如图所示,若a光是由能级n=4向n=l跃迁时发出时,则b光可能是( ) (2010?天津模拟)如图所示,真空中有一个固定的点电荷,电荷量为+Q,虚线表示该点电荷电场中的等势面.两个一价离子M、N(不计重力和它们之间的电场力)先后从a点以相同的速率v0射入该电场,运动轨迹分别为曲线a→b和a→c,其中b、c两点在同一等势面上,p、q分别是它们离固定点电荷最近的位置.下列说法中正确的是( )
(2010?天津模拟)如图所示,真空中有一个固定的点电荷,电荷量为+Q,虚线表示该点电荷电场中的等势面.两个一价离子M、N(不计重力和它们之间的电场力)先后从a点以相同的速率v0射入该电场,运动轨迹分别为曲线a→b和a→c,其中b、c两点在同一等势面上,p、q分别是它们离固定点电荷最近的位置.下列说法中正确的是( ) (2010?天津模拟)放在粗糙水平面上的物体A上叠放着物体B.A和B之间有一压缩的弹簧.A、B均处于静止状态,下列说法中正确的是( )
(2010?天津模拟)放在粗糙水平面上的物体A上叠放着物体B.A和B之间有一压缩的弹簧.A、B均处于静止状态,下列说法中正确的是( ) (2010?天津模拟)如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度的升高而减小.电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
(2010?天津模拟)如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin314t(V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2为用半导体热敏材料制成的传感器,其阻值随温度的升高而减小.电流表A2为值班室的显示器,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )