题目内容
 如图所示电路中,电源电动势E=10V,内电阻不计,电阻R1=14Ω,R2=6.0Ω,R3=2.0Ω,R4=8.0Ω,R5=10Ω,电容器的电容C=2.0 μF.求:
如图所示电路中,电源电动势E=10V,内电阻不计,电阻R1=14Ω,R2=6.0Ω,R3=2.0Ω,R4=8.0Ω,R5=10Ω,电容器的电容C=2.0 μF.求:(1)电容器所带的电量?说明电容器哪个极板带正电?
(2)若R1突然断路,将有多少电荷通过R5?.
分析:(1)当电路稳定时,R1与R2串联,R3与R4串联,两条支路并联.R5上没有电流流过.根据欧姆定律求解,结合电路电势关系求出a、b两点间的电势差,即为电容器的电压,再求电量.
(2)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压,根据电容器上电压的变化判断电容器充电或放电,分析通过R5的电荷.
(2)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压,根据电容器上电压的变化判断电容器充电或放电,分析通过R5的电荷.
解答:解:(1)设Ud=0,电容器两板间的电压即为a、b两点间的电势差.
则a点电势为Ua=Ud+
=0+
V=3 V.
电流由b点经R4流到d点,则b点电势为Ub=Ud+
=0+
V=8 V,
由Ub>Ua可知,电容器下板带正电.
b、a两点间的电势差Uba=Ub-Ua=5.0 V,电容器所带的电量为Q=CUba=1.0×10-5C.
(2)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压.
此时电容器所带电量Q′=CU4=C×
=2×10-6×
C=1.6×10-5 C.
由Ub>Ud可知,电容器下板仍带正电.
由Q′>Q知,R1断路后电容器经历了一次再充电过程,电容器极板上增加的电量为
△Q=Q′-Q=(1.6×10-5-1.0×10-5) C=6.0×10-6 C.
答:(1)电容器所带的电量为1.0×10-5C,电容器下板带正电.
(2)若R1突然断路,将有6.0×10-6 C电荷通过R5.
则a点电势为Ua=Ud+
| ER2 |
| R1+R2 |
| 10×6 |
| 14+6 |
电流由b点经R4流到d点,则b点电势为Ub=Ud+
| ER4 |
| R3+R4 |
| 10×8 |
| 2+8 |
由Ub>Ua可知,电容器下板带正电.
b、a两点间的电势差Uba=Ub-Ua=5.0 V,电容器所带的电量为Q=CUba=1.0×10-5C.
(2)R1断路,当再度达到稳定后,电容器电压等于R4两端的电压.
此时电容器所带电量Q′=CU4=C×
| ER4 |
| R3+R4 |
| 10×8 |
| 2+8 |
由Ub>Ud可知,电容器下板仍带正电.
由Q′>Q知,R1断路后电容器经历了一次再充电过程,电容器极板上增加的电量为
△Q=Q′-Q=(1.6×10-5-1.0×10-5) C=6.0×10-6 C.
答:(1)电容器所带的电量为1.0×10-5C,电容器下板带正电.
(2)若R1突然断路,将有6.0×10-6 C电荷通过R5.
点评:本题是电路桥式电路,对于电容器,关键求电压.本题电路稳定时,电容器的电压等于电容器这一路同侧两个电阻的电压之差.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
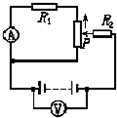 如图所示电路中,电源内阻不能忽略,R1阻值等于滑动变阻器总阻值的
如图所示电路中,电源内阻不能忽略,R1阻值等于滑动变阻器总阻值的| 3 |
| 4 |
| A、电压表的示数始终小于U |
| B、电流表的示数始终大于I |
| C、电压表的示数先增大后减小 |
| D、电流表的示数先减小后增大 |
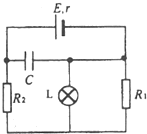 在如图所示电路中,电源的电动势、内阻恒定,要想使电容器所带的电荷量增加,可以采取的办法是( )
在如图所示电路中,电源的电动势、内阻恒定,要想使电容器所带的电荷量增加,可以采取的办法是( )| A、增大R2 | B、减小R2 | C、减小R1 | D、灯泡L短路 |
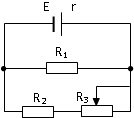 在如图所示电路中,电源的电动势是E,内电阻是r,当滑动变阻器R3的滑动头向左移动时( )
在如图所示电路中,电源的电动势是E,内电阻是r,当滑动变阻器R3的滑动头向左移动时( )| A、电阻R1的功率将减小 | B、电阻R2的功率将增大 | C、电源的功率将加大 | D、电源的效率将增加 |
 在如图所示电路中,电源电动势为E、内阻为r,R2、R3、R4均为定值电阻,电表都为理想电表.闭合电键S,当滑动变阻器R1的滑片P向右移动时,下列说法中正确的是( )
在如图所示电路中,电源电动势为E、内阻为r,R2、R3、R4均为定值电阻,电表都为理想电表.闭合电键S,当滑动变阻器R1的滑片P向右移动时,下列说法中正确的是( ) 如图所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω.若在C、D问连接一个电表或用电器,则有( )
如图所示电路中,电源电动势E=12V,内阻r=2Ω,R1=4Ω,R2=6Ω,R3=3Ω.若在C、D问连接一个电表或用电器,则有( )