题目内容

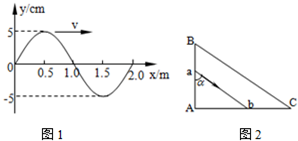
如图2所示，ab是半径为L、电阻不计的1/4圆周的金属槽环，固定于竖直平面内，圆心为O．Oa是质量不计的轻金属杆，其电阻为r，它的一端挂在O点（无摩擦），另一端连一金属小球，小球的质量为m，与金属槽环接触良好且无摩擦，Ob是一根竖直的与金属槽环相连接的金属丝，其电阻为R．上述整个装置置于水平方向垂直纸面向里的匀强磁场中，磁感应强度为B．现将金属小球从a点由静止开始释放，它滑到b点时的速度为v，所经过的时间为t．问这一过程中，感应电动势的有效值是多大？


本题以能量守恒定律、焦耳定律为知识依托，考查对有效值概念的理解能力．
先由能量守恒定律求出回路中产生的电能Q，即
mgL=mv2/2+Q
而此电能由焦耳定律知Q＝t，式中E为感应电动势的有效值．
由以上两式解得  E＝
【试题分析】
练习册系列答案
相关题目
（1）下列说法中正确的是
B
B

A．当某列声波产生多普勒效应时，相应声源的振动频率一定发生变化
B．狭义相对论指出：电磁相互作用在真空中的传播速度c是自然界中速度的极限
C．家用微波炉的工作应用了一种电磁波，而军用雷达的工作应用了一种脉冲超声波
D．大豆色拉油中的气泡看起来特别明亮，是因为光从气泡射向油时，一部分光在界面上发生了全反射的缘故
（2）如图1所示，实线是一列简谐横波在t1=0时的波形图，虚线为t2=0.5s时的波形图，已知0＜t2-t1＜T，t1=0时，x=2m处的质点A正向y轴正方向振动．
①波速大小为
2m/s
2m/s
；
②从t2时刻计时，x=1m处的质点的振动方程是
x=0.05sin（πt-
π
2
）
x=0.05sin（πt-
π
2
）

（3）如图2所示，AOB为半圆形玻璃砖截面，玻璃的折射率为n=
2
，现有一束平行光线以45°角入射到AB面上后，经折射从半圆面上的部分位置射出．试求半圆柱面能被照亮的部分与整个半圆柱面的面积之比．
选做题（请从A、B和C三小题中选定两小题作答，并在答题卡上把所选题目对应字母后的方框涂满涂黑．如都作答则按A、B两小题评分．）
A． （选修模块3-3）
（1）一定质量的理想气体发生等容变化，下列图象正确的是
C
C
．
（2）将剩有半杯热水的玻璃杯盖子旋紧后经过一段时间，若玻璃杯盖子不漏气，则杯内水蒸汽分子内能
减小
减小
  （填“增大”、“减小”或“不变”），杯内气体压强
减小
减小
  （填“增大”、“减小”或“不变”）．
（3）如图气缸放置在水平地面上，缸内封闭一定质量的理想气体，活塞横截面积为S，外界大气压强为p0，气缸内电热丝热功率为P，测得通电时间t内活塞缓慢向左移动距离为h，气缸向外界放出热量为Q，不计活塞与气缸之间的摩擦，则在时间t内缸内气体内能的变化量为
Pt-p0Sh-Q
Pt-p0Sh-Q
．

B．（选修模块3-4）
（1）下列说法中正确的是
D
D

A．X射线穿透物质的本领比γ射线更强
B．在电磁波发射技术中，使电磁波随各种信号而改变的技术叫做调谐
C．同一列声波在不同介质中传播速度不同，光波在不同介质中传播速度相同
D．爱因斯坦狭义相对论指出：真空中的光速在不同的惯性参考系中都是相同的
（2）如图1所示是一列沿x轴正方向传播的简谐横波在t=0时刻的波形图，已知波的传播速度v=2m/s．试回答下列问题：

①写出x=0.5m处的质点做简谐运动的表达式：
y=5cos2πt
y=5cos2πt
 cm；
②x=0.5m处质点在0～5.5s内通过的路程为
110
110
   cm．
（3）（4分）直角玻璃三棱镜的截面如图2所示，一条光线从AB面入射，ab为其折射光线，ab与AB面的夹角α=60°．已知这种玻璃的折射率n
2
，则：
①这条光线在AB面上的入射角为
45°
45°
；
②图中光线ab
不能
不能
（填“能”或“不能”）从AC面折射出去．
C． （选修模块3-5）幅图涉及到不同的物理知识，其中说法正确的是
AB
AB
 
A．图甲：普朗克通过研究黑体辐射提出能量子的概念，成为量子力学的奠基人之一
B．图乙：玻尔理论指出氢原子能级是分立的，所以原子发射光子的频率也是不连续的
C．图丙：卢瑟福通过分析α粒子散射实验结果，发现了质子和中子
D．图丁：根据电子束通过铝箔后的衍射图样，可以说明电子具有粒子性
（2）（4分）目前核电站是利用核裂变产生的巨大能量来发电的．请完成下面铀核裂变可能的一个反应方程：
 
235
52
U
+
1
0
n
→
141
56
Ba
+
92
36
Kr+
310n
310n
．已知
 
235
52
U、
 
141
56
Ba、
 
92
36
Kr和中子的质量分别为m1、m2、m3和m4，则此反应中一个铀核裂变释放的能量为
(m1-m2-m3-2m4)c2
(m1-m2-m3-2m4)c2
；
（3）一同学利用水平气垫导轨做《探究碰撞中的不变量》的实验时，测出一个质量为0.8kg的滑块甲以0.4m/s的速度与另一个质量为0.6kg、速度为0.2m/s的滑块乙迎面相撞，碰撞后滑块乙的速度大小变为0.3m/s，此时滑块甲的速度大小为
0.025
0.025
 m/s，方向与它原来的速度方向
相同
相同
（选填“相同”或“相反”）．
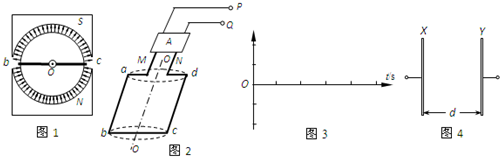精英家教网某种小发电机的内部结构平面图如图1所示，永久磁体的内侧为半圆柱面形状，它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小近似均匀的磁场，磁感应强度B=0.5T．磁极间的缺口很小，可忽略．如图2所示，单匝矩形导线框abcd绕在铁芯上构成转子，ab=cd=0.4m，bc=0.2m．铁芯的轴线OO′在线框所在平面内，线框可随铁芯绕轴线转动．将线框的两个端点M、N接入图中装置A，在线框转动的过程中，装置A能使端点M始终与P相连，而端点N始终与Q相连．现使转子以ω=200π rad/s角速度匀速转动．在图1中看，转动方向是顺时针的，设线框经过图1位置时t=0．（取π=3）
（1）求t=
1400
s时刻线框产生的感应电动势；
（2）在图3给出的坐标平面内，画出P、Q两点电势差UPQ随时间变化的关系图线（要求标出横、纵坐标标度，至少画出一个周期）；
（3）如图4所示为竖直放置的两块平行金属板X、Y，两板间距d=0.17m．将电压UPQ加在两板上，P与X相连，Q与Y相连．将一个质量m=2.4×10-12kg，电量q=+1.7×10-10C的带电粒子，在t0=6.00×10-3s时刻，从紧临X板处无初速释放．求粒子从X板运动到Y板经历的时间．（不计粒子重力）
某种小发电机的内部结构平面图如图1所示，永久磁体的内侧为半圆柱面形状，它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小近似均匀的磁场，磁感应强度B=
1
2π
T．磁极间的缺口很小，可忽略．如图2所示，单匝矩形导线框abcd绕在铁芯上构成转子，ab=cd=0.4m，bc=0.3m．铁芯的轴线OO′在线框所在平面内，线框可随铁芯绕轴线转动．将线框的两个端点M、N接入图中装置A，在线框转动的过程中，装置A能使端点M始终与P相连，而端点N始终与Q相连．现使转子以ω=200π rad/s的角速度匀速转动．在图1中看，转动方向是顺时针的，设线框经过图1位置时t=0．

（1）求t=
1
400
s时刻线框产生的感应电动势；
（2）在图3给出的坐标平面内，画出P、Q两点电势差UPQ随时间变化的关系图线（要求标出横、纵坐标标度，至少画出一个周期）；
（3）如图4所示为竖直放置的两块平行金属板X、Y，两板间距d=0.17m．将电压UPQ加在两板上，P与X相连，Q与Y相连．将一个质量m=1.2×10-12kg，电量q=+1.7×10-10C的带电粒子，在t0=6.00×10-3s时刻，从紧临X板处无初速释放．求粒子从X板运动到Y板经历的时间．（不计粒子重力）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网