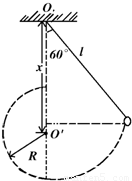
题目内容
 用长lm的细线系一个质量为0.1kg的小球做成一个摆,将它悬挂于O点,拉开小球使线与竖直方向成60°角时轻轻放开.若细线能承受的最大拉力为21N,那么要在悬挂点的正下方的什么距离范围内固定一根能阻挡细线的钉子,才能既保证线不断掉,又保证小球能绕钉子作一个完整的圆周运动?(g取10m/s2)
用长lm的细线系一个质量为0.1kg的小球做成一个摆,将它悬挂于O点,拉开小球使线与竖直方向成60°角时轻轻放开.若细线能承受的最大拉力为21N,那么要在悬挂点的正下方的什么距离范围内固定一根能阻挡细线的钉子,才能既保证线不断掉,又保证小球能绕钉子作一个完整的圆周运动?(g取10m/s2)分析:对小球在小圆最低点时由向心力公式结合动能定理求出最小半径,进而求出半径的范围.
小球绕O′点在竖直面内做完整圆周运动的半径为r,恰能过最高点时速度为v0,根据向心力公式求出最高点速度,由水平到最高点,由根据机械能守恒得最大半径,
小球绕O′点在竖直面内做完整圆周运动的半径为r,恰能过最高点时速度为v0,根据向心力公式求出最高点速度,由水平到最高点,由根据机械能守恒得最大半径,
解答:解:小球摆至最低点速度为v
mgl(1-cosθ)=
mv2
线不断:有T-mg=m
解得:r=0.05m
x=l-r=0.95m
完整的圆周运动,最高点速度为v0
根据牛顿运动定律得:mg=m
根据机械能守恒得:
mv2=
mv02+2mgR
解得:R=0.2m x′=l-2R=0.6m
故在0.6m≤x≤0.95m时,才能既保证线不断掉,又保证小球能绕钉子做一完整的圆周运动.
答:在0.6m≤x≤0.95m时,才能既保证线不断掉,又保证小球能绕钉子做一完整的圆周运动.
mgl(1-cosθ)=
| 1 |
| 2 |
线不断:有T-mg=m
| v2 |
| r |
解得:r=0.05m
x=l-r=0.95m
完整的圆周运动,最高点速度为v0
根据牛顿运动定律得:mg=m
| ||
| R |
根据机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:R=0.2m x′=l-2R=0.6m
故在0.6m≤x≤0.95m时,才能既保证线不断掉,又保证小球能绕钉子做一完整的圆周运动.
答:在0.6m≤x≤0.95m时,才能既保证线不断掉,又保证小球能绕钉子做一完整的圆周运动.
点评:本题主要考查了根据机械能守恒及向心力公式的应用,要注意小球能最高点对速度有要求,在最低时绳子的拉力不能超过最大承受力,难度适中.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目